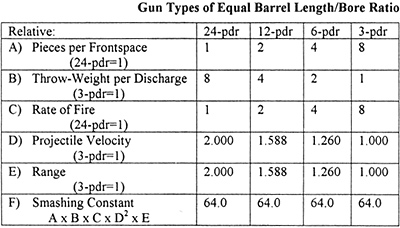
In the preceding section we deduced that for any given artillery design family or "system" characterized by barrel length/bore ratio, an octupling of cannonball weight coincides with a doubling of flight speed, such that a 24pound ball may be expected to have twice that of a 3-pound ball.

What effect does this have upon the guns' relative destructive powers?

Because a projectile's kinetic energy or "smashing power" increases with its weight or mass multiplied by the square of its velocity, the larger, faster ball's smashing power will be 8x (2 squared) or 32 times that of the smaller! On the other hand, because 8 times as many of the lighter guns will occupy the same width of front, (Edmondson, "Simulating Tactical Scenarios," SYWAJ, Vol. XII, No. 2, pages 47-48) and because each of these can fire 8 times as fast as the heavier piece, (Ibid. Page 60) the aggregate smashing power per unit time of an equal frontwidth's-worth of the lighter guns will be double that of the heavier (since 8x8=64) over its range half-as-long. A simplified table of relative fire effect for equal frontwidths of the two artillery types might therefore appear as follows:

Range	24-pdr	3-pdr
Short Range	32	64
Long Range	32	0
Total	64	64

Note: The particular values shown ("32", "64") are without significance in themselves, having been chosen simply for the sake of continuity with the foregoing text.

From a contemplation of the above, the astute reader will intuit the general principle that equal frontwidths-full of artillery, though of differing numbers of pieces, per-discharge throw-weight per piece, and range, may be expected to deliver equal cumulative smashing power upon a hostile force advancing upon the guns at a steady speed through the entirety of their respective ranges.

This is to say that the difference in performance between equal frontwidths of one artillery type and another boils down to the distribution of this "Smashing Constant" ("64" in the above illustration) over the intervals of time/distance marched by said hostile force, (Well, almost: there is also the matter of the heavier artillery's greater endurance (measured in per-day firing time, not in rounds) due to its lower rate of fire.) the intensity of the smashing power delivered per unit time ("32" for the 24-pounders and "64" for the 3-pounders in the above illustration) upon any such distance interval being equal to this "Smashing Constant" divided by each type's range.

The general principle having been grasped, it may be modified in application for (1) the employment of grapeshot and canister in place of roundshot at shorter distances, and (2) the increasing divergence from intended flight paths to be expected of any projectiles as the outer limits of range are approached - this latter being the chief source of difference between so-called "maximum" and "effective" ranges. These influences, while skewing the distribution of inflicted damage toward the shorter distances, still will not alter the fundamental condition of equality in cumulative smashing power delivered (upon a steadily advancing enemy over the entirety of its approach) by equal frontwidths-worth of different artillery types, provided that the relevant multipliers are applied to equal fractions of their respective ranges. (There exists yet another source of skewing of fire effect toward the lesser ranges: projectile flightspeed is not uniform over its range. Air resistance causes a cannonball's instantaneous flightspeed - and so its smashing power - to decline with distance flown. Further, this speed gradient is the steeper the lighter the cannonball (which is why the propellant-to-cannonball weight ratio need be higher for the lighter guns in order to achieve ranges in the same proportion to barrel length as for the heavier {refer again to Footnote 2 above)). Accordingly, it is to be expected that the lighter and shorter-ranged the artillery, the greater the fraction of the "Smashing Constant" concentrated in the shortest fractions of said range!)

On a higher plane, it is entirely to be expected that equal frontwidths-worth of different artilleries would render equal average service given their equal operating costs denominated in horses-required-to-haul. (Edmondson, "Simulating Tactical Scenarios," SYWAJ, Vol. XII, No. 2, pages 47-50 & 63-65)

Designs of unambiguously inferior utility for their barrel weight would have been scrapped (or at least demobilized) so as to concentrate scarce horsepower upon the others.

Accordingly, this fundamental condition of equality may be extended across artillery types whose projectiles are distinguished not only by count and weight and velocity, but also by flight trajectory and mode-of-action (blasting vs. smashing) - that is, to include howitzers.

However, this "equal average service" need not be found wholly in antipersonnel effect, for an equality in aggregate smashing power delivered does not necessarily translate into an equality in casualties inflicted: As the guns become weightier, the ever more focused smashing power of their fewer, heavier, higher velocity projectiles must be of declining utility against such soft, diffuse targets as the enemy horse and foot, even as its value against fortifications climbs. From this cause flows the virtual exclusion from the battlefield of pieces of barrel weights exceeding 4000 pounds. It is therefore appropriate that the lighter, shorter-ranged artilleries be accorded anti-personnel capabilities disproportionately great relative to their Smashing Constant/range ratios (which are of course greater over their shorter ranges to begin with). In the absence of good evidence as to its real extent, the precise degree of this disproportion must be left to the taste of the game designer.

It should also be understood that such "equal average service" data does not necessarily extend across nationalities. Different artillery types compete for funding (horses) only within and among those actually available to a particular state. Further, and perhaps more significantly, different armies' gunners may achieve different standards of professionalism, and so extract different levels of performance from equivalent hardware. Duffy suggests that the Austrian artillerists surpassed the others in this regard, and that this Austrian superiority expressed itself more in higher rates of fire than in the lengthening of effective ranges.

(Of course, one might "spin" this rapidity of fire as evidence of a lack of coolness. In a passage that appears to have been slightly garbled, Duffy (Instrument of War, page 416) quotes the report of a contemporary military critic: "Whenever I saw the Austrian artillery in action, its effect by far surpassed that of the Prussians, but I also observed that they preferred accurate (sic: I suspect the word `rapid' was intended) fire to taking leisurely and accurate aim, and opened up at extreme range with both roundshot and canister. Experienced officers recognize this fault, and do what they can to remedy it.")

Having resolved these issues to his own satisfaction, the game designer may proceed to develop tables of fire effect-by-rangespan for frontswidths'-worth or "batteries" of mixed gun types by calculating a weighted average effect for each span. Recurring to the example involving 24- and 3-pounder guns used at the beginning of this section, a simplified table of fire effect for a mixed battery thereof, equally weighted between the two types - that, is with eight 3-pounders for every one 24-pounder - might appear as follows:

Short Range 48 (= 32/2 plus 64/2)
Long Range 16 (= 32/2) Total 64

Comparative Performance of Seven Years War Artilleries

Introduction
Relative Ranges
Relative Destructive Power within Range
Concluding Caveats and Sources

This article appears in MagWeb.com (Magazine Web) on the Internet World Wide Web.
Other articles from military history and related magazines are available at http://www.magweb.com