As explosives go, gunpowder is relatively slow-burning. Its propulsive action upon a missile within a cannon barrel is not so much that of a mallet striking a croquet ball, as it is that of a hunter's breath pushing a dart through a blow gun - that is, it results from the expansion of gases released by the powder's combustion. This means that the muzzle velocity imparted to the projectile is a function of (1) the ratio of propellant to barrel interior volume, and (2) absolute barrel length. The first is limited by lateral barrel strength or `robustness." Controlling for the first, muzzle velocity will be driven by the second (barrel length) alone.
Given that the volume of a cannonball (a sphere) varies as the cube of the diameter, and that the volume of the interior of a gun barrel (a cylinder) varies as the square of its bore times its length, and assuming constant ratios of ball weight/volume, barrel length/bore (in "calibers"), propellant weight/ball weight, and gas volumes released/propellant weight/time elapsed post-ignition, then any multiplication of cannonball weight produces directly proportional increases in both barrel volume and propellant gas volumes released per unit time postignition, co-incident with an increase in barrel length and, therefore, cannonball speed out-the-barrel equal to the cube-root of the cannonball weight multiplier.
This is to say that within any gun design family of characteristic barrel length bore ratio, each doubling of per-discharge throw-weight produces a doubling of cannon barrel volume along with an increase in barrel length to (cubed root of 2) or 1.26 times the original. And if, as might be achieved by doubling likewise the weight of charge, the gas volumes released there from fill said doubly voluminous, 1.26 times-as-long barrel in the same time elapsed post-ignition, then the ball must be pushed through it at 1.26 times the speed, and so in the absence of air resistance fly 1.26 (say 5/4) times the distance before falling to earth, assuming both gun barrels to be equidistant from, and parallel to, the ground. [This is not to say that a cannonball's capacity to work destruction was necessarily ended by its first contact with the ground, but only that its flight distance to that point provides a conceptually convenient basis of comparison.]
Similarly, each octupling of throw-weight will produce a doubling of range. (Multiplying throw-weight by 3/2 produces a x 8/7 effect on range; multiplying throw-weight by 4/3 produces a x 11/12 effect on range, etc.)
Complicating the relationship between muzzle velocity and range is the effect of air resistance, which, applied to spherical projectiles of uniform weight-per-volume, operates to compress the spread of ranges otherwise to be expected between faster and slower projectiles (controlling for weight), while widening the spread of ranges between heavier and lighter projectiles (controlling for initial speed). Because the latter influence is more pronounced than the former, the limiting of the increase in range to our hypothesized 5/4 factor for each doubling of ball weight would require that the weight of propellant not be doubled as well, but increased by some slightly lesser multiple. And such, in fact, appears to have been the practice:
- Weight-of-charge increased by about 13/e times for each doubling of projectile weight within a gun design family. Duffy, Instrument of War, pages 284-285, reports the following charges for 16-caliber Austrian pieces:
| Type | Charge Max | Charge/Ball Ratio |
|---|---|---|
| 3-pounder | 14 to 16 Oz. | 1/3 |
| 6-pounder | 20 to 28 Oz. | 7/24 |
| 12-pounder | 40 to 48 Oz. | 1/4 |
The 12-pounder's charge weight/ball weight ratio of 1/4 is facially at variance with statements made in Duffy, Fire and Stone, that 12-, 18-, and 24-pounder siege and fortress guns required powder in the ratio of 1/3 weight-of-shot, as well as in Duffy, Russia's Military Way to the West, page 71, that the highest charge weight/ball weight ratio seen was 1/2. However, it seems likely that the siege and fortress artillery discussed in the former were Valliere or Brummer types of 22 calibers length or longer, which would confirm a propellant-to-shot ratio of about 1/3 (1/4 x 22/16) after all, if propellant be increased in proportion to length within artillery types characterized by per-discharge throw-weight. Similarly might the charge for long-barreled 3-pounders approximate 1/2 the weight of shot ((22 to 26)/16 x 1/3) as mentioned in the latter.
A practice to the extent that the gun ranges by throw-weight reported in various contexts do show after all a remarkable consistency with the 6 1/4 to 5 to 4 ratio for 12- to 6- to 3-pounders predicted per our original formula without regard to air resistance. And as go the ranges, so also must go the average flight speeds, given that all cannonballs projected horizontally from the same height must fall to earth in the same elapsed time.
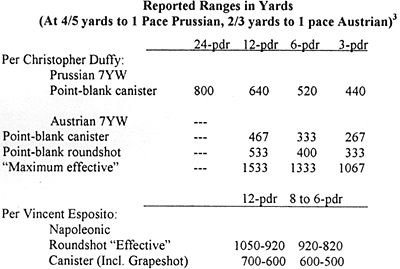
3: Data from Duffy, Army of Frederick the Great, page 176, Instrument of War, pages 284-285, and Esposito, Atlas of Napoleonic Wars.
As a corollary to the above we may deduce that within any class of guns characterized by per-discharge throw-weight, an increase in barrel length accompanied by a proportionate increase in weight of propellant might be expected to produce a proportionate effect upon muzzle velocity and range if the increased air resistance could be overcome, as by the addition of still more propellant. If so, then a 26-calibers-long "Fortress Brummer" 12-pounder might be expected to have 26/16 the range of a 16-calibers-long "Austrian" 12pounder,
But simply ignoring air resistance - or blithely assuming the gun barrels to be in every case sufficiently robust as to stand the addition of propellant-enough to compensate for it - is not really satisfactory. Consider, for instance what I have elsewhere termed the "Prussian light" family - a thin-walled breed whose true ranges relative to those of the heavier "Austrian" family were doubtless markedly less than those predicted on the basis of barrel length alone. So unsuited indeed were the "Light Dieskau" 12-pounders for battery work as to cause them to be banished to the infantry!
As for the aforementioned "Fortress Brummer," I suspect the power of air resistance to be such that even with more than 26/16 the propellant charge, its range would still have been a tad less than 26/16 that of the Austrian 12-pounder.
Physicists from Isaac Newton onward have struggled without success to devise a universally valid mathematical formula to predict the effect upon prosjectile speed of the interplay between barrel design and air resistance. In the 19` century these efforts were largely abandoned in favor of the brute range testing of particular gun models, one at a time. Lacking access to such costly methods, we are thrown back upon theoretical approaches.
A viable alternative approach to the determination of ranges on the basis of simple barrel length would be one based upon barrel weight (weight being a function of both length and robustness), making it the driver of range not only within, but across design families, such that a super-heavy 4,000 lb. 12-pounder would have just 5/4 the range of a 2,000 lb. "Austrian" model, while a "light Dieskau" 12-pounder, an "Austrian" 6-pounder, and a Valliere 4-pounder, each weighing about 1,000 lbs., would have all about 4/5 the range of the Austrian 12-pounder gun - down from the 14/16 thereof for the 14-calibers-long "light Dieskau" under the unadorned barrel-length approach.
Nor should we stop there. Any given weight of barrel-bronze, reconfigured from one gun to another of greater bore diameter, is bound to produce a new barrel shorter than the old, controlling for wall-thickness. Consider for example a 22-calibers-long 3-pounder gun, melted down and recast as a 5 1/2-calibers-long 24-pounder (iron weight) howitzer: though with double the interior volume of the former, the new piece would be just half as long, meaning that even with a weight-of-charge in the same proportion to interior volume (that is, double the absolute amount, or one-quarter the amount relative to the volume of the projectile), the howitzer attains only one-half the muzzle velocity of the gun (fired horizontally).
To generalize this effect across all such barrel weight-translations requires that the range (before adjusting for air resistance) for any piece be set equal to that of the equivalent-barrel-weight gun of the design family (I use the "Austrian") chosen as standard, multiplied by the ratio of said range to that of the equivalent-throw-weight gun of the same (that is, the standard) design family. For the "Light Dieskau" 12-pounder, the formula would yield a range only 4/5 that of the equal-barrel-weight "Austrian" 6 pounder, or 4/6'25 (= 5/6..25 x 5/6.25) that of the "Austrian" 12-pounder - that is, equal to an "Austrian" 3-pounder, a battalion gun.
No wonder the frail "Light Dieskau" was banished to the infantry! Recall, however, that air resistance tends to compress the ranges of guns of equal throw-weight (about the chosen standard); accordingly, the air resistance-adjusted range of the "Light Dieskau" 12-pounder was probably a bit more than 4/6.25, though less than 5/6.25, that of the Austrian. Similarly might the range of the "Fortress Brummer" 12-pounder fall somewhere between 25/16 and 5/4 that of the "Austrian."
In view of the foregoing discussion, the following table of relative ranges and/or flightspeeds expected for SYW artillery pieces, based solely on barrel length, must be used with caution, especially with respect to comparisons across design families of greatly differing robustness.
Relative Ranges (Taking That for a 16-Calibers-Long Austrian 3-Pounder as "1.00") By Actual (Gun) and/or Implied (Howitzer) Per-Discharge Throw-Weight
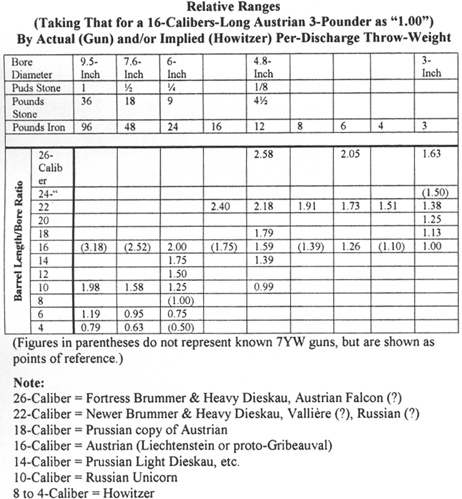
- (Figures in parentheses do not represent known 7YW guns, but are shown as points of reference.)
Note:
- 26-Caliber = Fortress Brummer & Heavy Dieskau, Austrian Falcon (?)
22-Caliber = Newer Brummer & Heavy Dieskau, Valliere (?), Russian (?)
18-Caliber = Prussian copy of Austrian
16-Caliber = Austrian (Liechtenstein or proto-Gribeauval)
14-Caliber = Prussian Light Dieskau, etc.
10-Caliber = Russian Unicorn
8 to 4-Caliber = Howitzer
It may be objected that the hypothesized progression of ranges for pieces of like throw-weight across the many barrel length/bore ratios should not extend to the lower levels thereof, these being "howitzers," whose projectiles' more arcing flight paths might be expected to carry them much farther than those of equivalent flat-trajectory pieces. Indeed, compared to a cannon with barrel 4 feet above and parallel to the ground, such that its projectile first hits the earth '/2 second after leaving the muzzle (cumulative distance fallen = 16 feet x (# seconds) squared), a howitzer fired at 45° elevation with equal muzzle velocity and zero air resistance would hurl its projectile three-eighths the square of the distance-in-yards flown by the cannonball (before its first bounce).
- Setting R = Distance in yards flown by the gun's projectile in 1/2 second, then 2R = flightspeed per second, and 2R/(squareroot 2) = Horizontal distance traveled per second by howitzer projectile of 2R flightspeed fired at 45° elevation, and [2R/(squareroot 2)]/5 1/3 = Number of seconds flown by said howitzer projectile, and [2R/(squareroot 2)] x [(2R/(squareroot 2)]/5 1/3) = 2R squared/5 1/3 = 3/8R squared = Horizontal distance flown by said howitzer projectile in yards.
"Equal muzzle velocity," however, does not obtain for howitzers owing to the large reductions in propellant necessary to prevent not only the cracking of their shell casings upon discharge, (Duffy, Army of Frederick the Great, page 174) but also the crushing of their wooden carriage wheels under the ever more downward-directed shock of recoil as the angle of elevation climbs - a serious limitation in the era before the adoption of iron wheels and axles, not to mention the hydraulic shock absorber. (Mortars, fired at even higher angles than howitzers, (Duffy, Ibid. Page 175) were not wheeled at all, but mounted on sturdy wooden platforms which disintegrated nonetheless under the repeated shocks; the substitution of platforms of solid iron in the latter part of the eighteenth century made possible a tremendous increase in weight-of-charge and, therefore, range for these weapons (Duffy, Fire and Stone, page 153)).
Further, even in relation to the reduced charges that high angle artillery could tolerate and still remain mobile, the muzzle velocity generated thereby would be lessened by the need to push against the force of gravity upon the projectile during its entire passage upwards through the barrel, whereas the propellant of guns fired at 0° elevation had need to overcome the force of inertia alone: imagine what greater strength is required to lift a heavy spherical object than merely to roll it over a firm, flat surface.
Moreover, once projected from the barrel, the howitzer shell not only was, slowed by air resistance, but slowed to a degree beyond that for a cannonball of equal diameter and muzzle velocity due to its lower weight-per-volume (about 3/4 that of the ball).
- (Edmondson, "Simulation of Tactical Scenarios," SYWAJ, Vol. XII, No. 2, page 63)
Accordingly, the special utility of Seven Years War howitzers as battlefield weapons was not an extraordinary range, but rather the ability to lob shells onto targets behind obstacles like breastworks and woods that would block the flight of a flat-trajectory projectile. In open country, howitzers were good mostly for firing grapeshot point blank, for which their wide bores eminently suited them and by which the need for reduced charges was obviated.
- (Duffy, Army of Frederick the Great, page 182)
But just what ranges could howitzers attain through high angle fire with reduced charges, compared to the flat trajectory, propellant-in-proportion-tobarrel-volume conditions assumed in constructing our table of relative ranges? Data furnished by Duffy for the Austrian "7-pounder" howitzer indicate that it had in fact a bore (6 inches) equal to that of a 24-pounder (iron weight) piece, ("153 mm" per Duffy, Instrument of War, page 285) and so despite its name would count as a 9-pounder or 1/4 pud (stone weight) piece in our table. But whereas at 6 calibers barrel length its table-predicted range would be only 0.75 that of a 16-caliber 3-pounder gun, Duffy specifies for this howitzer a "maximum effective" range of from 1.125 to 1.250 that of the gun, (Duffy, Instrument of War, pages 284-285, specifies a "maximum effective" range for a 16-caliber 3-pounder gun of 1600 paces and for a "7-pounder" howitzer of 1800 to 2000 paces) or 1 1/2 to 1 2/3 times the howitzer's 0.75 table value. It would seem not unreasonable to extend the application of this multiplier to the table-predicted ranges for other howitzer types, were it not for the assertion of Prince Liechtenstein, guiding light of the Austrian artillery, that the "7-pounder" howitzer possessed "a longer range than all the other calibers," (Duffy, Instrument of War, page 285) which implies that the aforementioned constraints upon howitzer muzzle velocity operated not merely to discount, but even to limit or reverse the progression of ranges through the 1/2-pud and 1-pud calibers favored by the Russians. (But how then to explain the amazing range (Duffy, Army of Frederick the Great, page 175) claimed for the post-war Prussian "10-pounder battery howitzer"? Iron axles? Puffery?)
Even more doubtful is the validity of applying such a multiplier to the table ranges for gun/howitzer hybrids like the 10-caliber "unicorns", as they appear not to have been designed for high-angle fire - at least with their wheels on: "When it was desired to fire unicorns at extreme ranges, the tubes were placed on special carriages that resembled ship carriages without the trucks." (Carpenter, "Russian Artillery," SYWAJ, Vol. X, No. 2, page 52)
Determining the relative range for the Shuvalov "secret howitzer" - which despite its name was a specialized canister-firing weapon, not built for high-angle fire at all - presents an entertaining challenge. Its oval bore had the vertical dimension of a 3-Founder (iron weight) gun, and the horizontal dimension of a 24-pounder; (Duffy, Russia's Military Way to the West, pages 69-70) its barrel length of 18 calibers relative to its vertical bore dimension equates to 9 calibers relative to the horizontal. Some writers suggest a compromise classification as a 12-pounder, (Carpenter, "Russian Artillery," SYWAJ. Vpl. X, No. 2, page 54) relative to which the same absolute barrel length would count as 11 1/4 calibers. Whichever way of the three you choose to regard it, its range according to our formula would be 1.125 that of a 16-caliber 3-pounder gun. But this would be for roundshot; the Shuvalov fired only grape and canister. ("An explosive shell could also be fired, but because the oval configuration of the barrel necessitated that it be flask-shaped, rather than round, it was neither long-ranged nor very accurate." Ibid, page 55. )
Applying what appears to be the typical ratio for grapeshot-to-roundshot range of 2/3, the Shuvalov's relative range figure of 1.125 becomes 0.750, which seems about right. (Duffy, Russia's Military Way to the West, pages 70-71, states that the Shuvalov's small-ball canister "spewed out to 300 paces," the large-ball canister "carried up to 600," and the grapeshot "ranged up to 1200 paces.")
Before leaving the subject of shorter-barreled artillery it should be noted that Esposito reports a spread of ranges for Napoleonic 6-inch (= 24-pounder iron weight) howitzers of unspecified barrel lengths of from 750 to 1300 yards, versus circa 1000 yards for a 12-pounder gun, which would make the high end (the 1300 yards) co-incident with the table-consistent value for a 16-caliber 24pounder gun (circa 1280 yards). The significance of this is unclear, particularly in view of the possibility that artillerists may by that era have fitted iron axles and wheels to their howitzers, abolishing their comparability to Seven Years War types.
Comparative Performance of Seven Years War Artilleries
Back to Seven Years War Asso. Journal Vol. XIII No. 1 Table of Contents
Back to Seven Years War Asso. Journal List of Issues
Back to Master Magazine List
© Copyright 2003 by James J. Mitchell
This article appears in MagWeb.com (Magazine Web) on the Internet World Wide Web.
Other articles from military history and related magazines are available at http://www.magweb.com