The influence of artillery changed significantly between the 17th Century and the 18th Century. One of the most important changes was the general standardisation of the bore size or weight of the projectile, mainly the round cannon ball, which allowed an army to minimise the types of munitions transported by the army (and the production of said munitions). Cannons for field use were normally 3-, 6-, 9-, 12- and 24-pounders and howitzers were normally 6-, 8-, 10- and 13-inch (British howitzers were 5.8-, 8- and 10- inch).

Another was the doctrine of artillery employment in battle. This changed the role of cannons from static units to manoeuvrable units, which could be deployed at various locations during the course of the battle, as needed.

A third was the scientific or technical studies of ballistics and the organisation of permanent artillery units instead of hiring civilian specialists. Once a system of general artillery doctrine was standardised, the types and roles of artillery remained unchanged until the second half of the 19th Century Much of the article is based on the information contained in “Artillery Through the Ages” by Albert Manucy (available from the US National Park Service). Other sources include rulebooks, several books by Christopher Duffy and others. Most of the information relates to ballistics so it is technical.

Gunpowder is relatively slow burning, thus its propulsive action upon a cannon ball is not so much that of a cue stick hitting a billiard ball, as that of a hunter blowing on a dart in a blowgun. The expansion of gases released by the powder's combustion forces the ball to travel the barrel length and beyond.

In technical terms, it means that the muzzle velocity imparted to the projectile is a function of

(1) the ratio of propellant to barrel interior volume, and
(2) absolute barrel length.

The first is limited by lateral barrel strength or “robustness”. Controlling for the first, muzzle velocity will be driven by the second (barrel length) alone. Given that the volume of a cannonball (a sphere) varies as the cube of the diameter, and that the volume of the interior of a gun barrel (a cylinder) varies as the square of its bore times its length, and assuming constant ratios of ball weight/volume, barrel length/bore (in "calibres"), propellant weight/ball weight, and gas volumes released/propellant weight/time elapsed post-ignition, then any multiplication of cannonball weight produces directly proportional increases in both barrel volume and propellant gas volumes released per unit time post ignition, co-incident with an increase in barrel length and, therefore, cannonball speed out-the-barrel is equal to the cube-root of the cannonball weight multiplier.

Now say that quickly several times just to be further confused!

This is to say that within any gun design family of characteristic barrel length bore ratio, each doubling of per-discharge throw-weight produces a doubling of cannon barrel volume along with an increase in barrel length to (cubed root of 2) or 1.26 times the original. And if, as might be achieved by doubling likewise the weight of charge, the gas volumes released there from fill said doubly voluminous, 1.26 times-as-long barrel in the same time elapsed post-ignition, then the ball must be pushed through it at 1.26 times the speed, and so in the absence of air resistance fly 1.26 (say 5/4) times the distance before falling to earth, assuming both gun barrels to be equidistant from, and parallel to, the ground.

Similarly, each octupling of throw-weight will produce a doubling of range. (Multiplying throw-weight by 3/2 produces a x 8/7 effect on range; multiplying throw-weight by 4/3 produces a x 11/12 effect on range, etc.)

Complicating the relationship between muzzle velocity and range is the effect of air resistance, which, applied to spherical projectiles of uniform weight-per-volume, operates to compress the spread of ranges otherwise to be expected between faster and slower projectiles (controlling for weight), while widening the spread of ranges between heavier and lighter projectiles (controlling for initial speed). Because the latter influence is more pronounced than the former, the limiting of the increase in range to our hypothesized 5/4 factor for each doubling of ball weight would require that the weight of propellant not be doubled as well, but increased by some slightly lesser multiple. And such, in fact, appears to have been the practice:

Weight-of-charge increased by about 13/e times for each doubling of projectile weight within a gun design family. Duffy, Instrument of War, pages 284-285, reports the following charges for 16-caliber Austrian pieces:

Type	Charge	Max Charge/Ball Ratio
3-pounder	14 to 16 Oz.	1/3
6-pounder	20 to 28 Oz.	7/24
12-pounder	40 to 48 Oz.	1/4

The 12-pounder's charge weight/ball weight ratio of 1/4 is facially at variance with statements made in Duffy, Fire and Stone, that 12-, 18-, and 24-pounder siege and fortress guns required powder in the ratio of 1/3 weight-of-shot, as well as in Duffy, Russia's Military Way to the West, page 71, that the highest charge weight/ball weight ratio seen was 1/2. However, it seems likely that the siege and fortress artillery discussed in the former were Valliere or Brummer types of 22 calibres length or longer, which would confirm a propellant-to-shot ratio of about 1/3 (1/4 x 22/16) after all, if propellant be increased in proportion to length within artillery types characterized by per-discharge throw-weight. Similarly might the charge for long-barrelled 3-pounders approximate 1/2 the weight of shot ((22 to 26)/16 x 1/3) as mentioned in the latter.

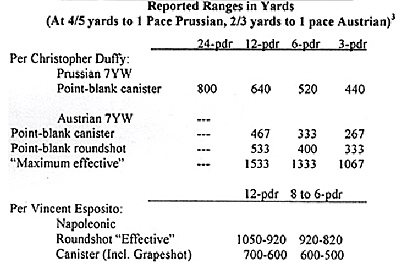A practice to the extent that the gun ranges by throw-weight reported in various contexts do show after all a remarkable consistency with the 6 1/4 to 5 to 4 ratio for 12- to 6- to 3- pounders predicted per our original formula without regard to air resistance. And as go the ranges, so also must go the average flight speeds, given that all cannonballs projected horizontally from the same height must fall to earth in the same elapsed time.

Chart Data: 3: Data from Duffy, Army of Frederick the Great, page 176, Instrument of War, pages 284-285, and Esposito, Atlas of Napoleonic Wars.

As a corollary to the above we may deduce that within any class of guns characterized by per-discharge throw-weight, an increase in barrel length accompanied by a proportionate increase in weight of propellant might be expected to produce a proportionate effect upon muzzle velocity and range if the increased air resistance could be overcome, as by the addition of still more propellant. If so, then a 26-calibres-long "Fortress Brummer" 12- pounder might be expected to have 26/16 the range of a 16-calibres-long "Austrian" 12-pounder.

But simply ignoring air resistance - or blithely assuming the gun barrels to be in every case sufficiently robust as to stand the addition of propellant-enough to compensate for it is not really satisfactory. Consider, for instance what has been elsewhere termed the "Prussian light" (or Light Dieskau) family - a thin-walled breed whose true ranges relative to those of the heavier "Austrian" family were doubtless markedly less than those predicted on the basis of barrel length alone. So unsuited indeed were the "Light Dieskau" 12-pounders for battery work as to cause them to be assigned to the infantry as “battalion guns”.

Physicists from Isaac Newton onward have struggled without success to devise a universally valid mathematical formula to predict the effect upon projectile speed of the interplay between barrel design and air resistance. In the 19th Century these efforts were largely abandoned in favour of the brute range testing of particular gun models, one at a time. Lacking access to such costly methods, we are thrown back upon theoretical approaches.

A viable alternative approach to the determination of ranges on the basis of simple barrel length would be one based upon barrel weight (weight being a function of both length and robustness), making it the driver of range not only within, but across design families, such that a super-heavy 4,000 lb. 12-pounder would have just 5/4 the range of a 2,000 lb. "Austrian" model, while a "light Dieskau" 12-pounder, an "Austrian" 6-pounder, and a Valliere 4-pounder, each weighing about 1,000 lbs., would have all about 4/5 the range of the Austrian 12-pounder gun - down from the 14/16 thereof for the 14-calibres-long "light Dieskau" under the unadorned barrel-length approach.

Any given weight of barrel-bronze, reconfigured from one gun to another of greater bore diameter, is bound to produce a new barrel shorter than the old, controlling for wall-thickness. Consider for example a 22-calibers-long 3-pounder gun, melted down and recast as a 5 1/2-calibers-long 24-pounder (iron weight) howitzer: though with double the interior volume of the former, the new piece would be just half as long, meaning that even with a weight-of-charge in the same proportion to interior volume (that is, double the absolute amount, or one-quarter the amount relative to the volume of the projectile), the howitzer attains only one-half the muzzle velocity of the gun (fired horizontally). To generalize this effect across all such barrel weight-translations requires that the range (before adjusting for air resistance) for any piece be set equal to that of the equivalent-barrel- weight gun of the design family (hereafter using "Austrian" artillery as the models) chosen as standard, multiplied by the ratio of said range to that of the equivalent-throw-weight gun of the same (that is, the standard) design family. For the "Light Dieskau" 12-pounder, the formula would yield a range only 4/5 that of the equal-barrel-weight "Austrian" 6 pounder, or 4/6'25 (= 5/6..25 x 5/6.25) that of the "Austrian" 12-pounder -- that is, equal to an "Austrian" 3-pounder, a battalion gun.

No wonder the frail "Light Dieskau" was given to the infantry! Recall, however, that air resistance tends to compress the ranges of guns of equal throw-weight (about the chosen standard); accordingly, the air resistance-adjusted range of the "Light Dieskau" 12-pounder was probably a bit more than 4/6.25, though less than 5/6.25, that of the Austrian.

In view of the foregoing discussion, the following table of relative ranges and/or flight speeds expected for SYW artillery pieces, based solely on barrel length, must be used with caution, especially with respect to comparisons across design families of greatly differing robustness.

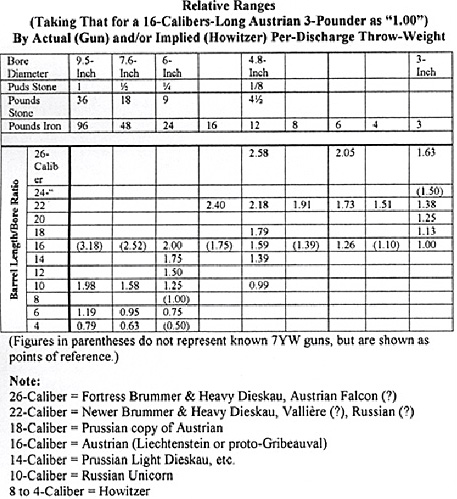Relative Ranges (Taking That for a 16-Calibers-Long Austrian 3-Pounder as "1.00") By Actual (Gun) and/or Implied (Howitzer) Per-Discharge Throw-Weight

"Effective" range being such a nebulous concept; the choice of a scale of absolute distances to be fitted to our table of relative ranges must be left to the judgement of the game designer. For this purpose, it is convenient to deal in battalion-widths of 160 yards (=200 Prussian paces, =240 Franco-Austrian). Fixing the effective range of an Austrian 16-calibre 3-pounder gun at 4 battalion-widths, for example, yields a range of 5 battalion-widths for an Austrian 6-pounder, and 6 1/4 battalion-widths or 1000 yards for an Austrian 12 pounder, which last figure corresponds most admirably to that reported by Esposito for the Napoleonic "Gribeauval System" 12-pounder, modelled upon the Seven Years War Austrian design. It also yields an effective range of 9 to 10 battalion-widths for the very heaviest guns likely to accompany a field army, which corresponds to the outermost distance (2000 Prussian paces) at which an enemy army advancing thereon might deploy from column into line, to avoid the devastation to be wrought by the impact of a cannonball down the length of a column. (Note the above information is derived from Nosworthy, Anatomy of Victory, page 287).

These calculations can only be applied to cannons and not to howitzers, which have a different performance because of trajectory and calibre.

Data furnished by Duffy for the Austrian "7-pounder" howitzer indicate that it had in fact a bore (6 inches) equal to that of a 24-pounder (iron weight) piece, ("153 mm" per Duffy, Instrument of War, page 285) and so despite its name would count as a 9-pounder or 1/4 pud (stone weight) piece in the above table. But whereas at 6 calibres barrel length its table-predicted range would be only 0.75 that of a 16-caliber 3-pounder gun, Duffy specifies for this howitzer a "maximum effective" range of from 1.125 to 1.250 that of the gun, (Duffy, Instrument of War, pages 284-285, specifies a "maximum effective" range for a 16-calibre 3-pounder gun of 1600 paces and for a "7-pounder" howitzer of 1800 to 2000 paces) or 1 1/2 to 1 2/3 times the howitzer's 0.75 table value.

It would seem not unreasonable to extend the application of this multiplier to the table-predicted ranges for other howitzer types, were it not for the assertion of Prince Liechtenstein, guiding light of the Austrian artillery, that the "7-pounder" howitzer possessed "a longer range than all the other calibres," (Duffy, Instrument of War, page 285) which implies that the aforementioned constraints upon howitzer muzzle velocity operated not merely to discount, but even to limit or reverse the progression of ranges through the 1/2-pud and 1-pud calibres favoured by the Russians.

Even more doubtful is the validity of applying such a multiplier to the table ranges for gun/howitzer hybrids like the 10-calibre "unicorns", as they appear not to have been designed for high-angle fire at least with their wheels, but rather when placed on special carriages.

Before leaving the subject of shorter-barrelled artillery it should be noted that Esposito reports a spread of ranges for Napoleonic 6-inch (= 24-pounder iron weight) howitzers of unspecified barrel lengths from 750 to 1300 yards, compared to about 1000 yards for a 12-pounder gun, which would make the high end (the 1300 yards) co-incident with the table-consistent value for a 16-calibre 24pounder gun (approximately 1280 yards). The significance of this is unclear, particularly in view of the possibility that artillerists may by that era have fitted iron axles and wheels to their howitzers, abolishing their comparability to Seven Years War types.

In the preceding section we deduced that for any given artillery design family or "system" characterized by barrel length/bore ratio, an octupling of cannonball weight coincides with a doubling of flight speed, such that a 24pound ball may be expected to have twice that of a 3-pound ball.

What effect does this have upon the guns' relative destructive powers? Because a projectile's kinetic energy or "smashing power" increases with its weight or mass multiplied by the square of its velocity, the larger, faster ball's smashing power will be 8x (2 squared) or 32 times that of the smaller! On the other hand, because 8 times as many of the lighter guns will occupy the same width of front, and because each of these can fire 8 times as fast as the heavier piece, the aggregate smashing power per unit time of an equal front width's-worth of the lighter guns will be double that of the heavier (since 8x8=64) over its range half-as-long. A simplified table of relative fire effect for equal front widths of the two artillery types might therefore appear as follows:

Range	24-pdr	3-pdr
Short	32	64
Long	32	0
Total	64	64

Note: The particular values shown ("32", "64") are without significance in themselves, having been chosen simply for the sake of continuity with the foregoing text. From a contemplation of the above, the astute reader will intuit the general principle that equal front widths-full of artillery, though of differing numbers of pieces, per-discharge throw-weight per piece, and range, may be expected to deliver equal cumulative smashing power upon a hostile force advancing upon the guns at a steady speed through the entirety of their respective ranges.

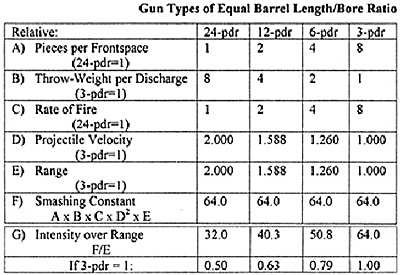This is to say that the difference in performance between equal front widths of one artillery type and another boils down to the distribution of this "Smashing Constant" ("64" in the above illustration) over the intervals of time/distance marched by said hostile force, (Well, almost: there is also the matter of the heavier artillery's greater endurance (measured in per-day firing time, not in rounds) due to its lower rate of fire.) the intensity of the smashing power delivered per unit time ("32" for the 24-pounders and "64" for the 3-pounders in the above illustration) upon any such distance interval being equal to this "Smashing Constant" divided by each type's range.

The general principle having been grasped, it may be modified in application for

(1) the employment of grapeshot and canister in place of round shot at shorter distances, and

(2) the increasing divergence from intended flight paths to be expected of any projectiles as the outer limits of range are approached -- this latter being the chief source of difference between so-called "maximum" and "effective" ranges.

These influences, while skewing the distribution of inflicted damage toward the shorter distances, still will not alter the fundamental condition of equality in cumulative smashing power delivered (upon a steadily advancing enemy over the entirety of its approach) by equal front widths-worth of different artillery types, provided that the relevant multipliers are applied to equal fractions of their respective ranges.

There is yet another source of skewing of fire effect toward the lesser ranges: projectile flight speed is not uniform over its range. Air resistance causes a cannonball's instantaneous flight speed -- and so its smashing power - to decline with distance flown. Further, this speed gradient is the steeper the lighter the cannonball (which is why the propellant-to-cannonball weight ratio needs be higher for the lighter guns in order to achieve ranges in the same proportion to barrel length as for the heavier. Accordingly, it is to be expected that the lighter and shorter-ranged the artillery, the greater the fraction of the "Smashing Constant" concentrated in the shortest fractions of said range!

Designs of unambiguously inferior utility for their barrel weight would have been scrapped (or at least demobilized) so as to concentrate scarce horsepower upon the others. Accordingly, this fundamental condition of equality may be extended across artillery types whose projectiles are distinguished not only by count and weight and velocity, but also by flight trajectory and mode-of-action (blasting vs. smashing) - that is, to include howitzers.

However, this "equal average service" need not be found wholly in antipersonnel effect, for an equality in aggregate smashing power delivered does not necessarily translate into an equality in casualties inflicted: As the guns become weightier, the ever more focused smashing power of their fewer, heavier, higher velocity projectiles must be of declining utility against such soft, diffuse targets as the enemy horse and foot, even as its value against fortifications climbs. From this cause flows the virtual exclusion from the battlefield of pieces of barrel weights exceeding 4000 pounds. It is therefore appropriate that the lighter, shorter-ranged artilleries be accorded anti-personnel capabilities disproportionately great relative to their Smashing Constant/range ratios (which are of course greater over their shorter ranges to begin with). In the absence of good evidence as to its real extent, the precise degree of this disproportion must be left to the taste of the game designer.

It should also be understood that such "equal average service" data does not necessarily extend across nationalities. Different artillery types compete for funding (horses) only within and among those actually available to a particular state. Further, and perhaps more significantly, different armies' gunners may achieve different standards of professionalism, and so extract different levels of performance from equivalent hardware.

Duffy suggests that the Austrian artillerists surpassed the others in this regard, and that this Austrian superiority expressed itself more in higher rates of fire than in the lengthening of effective ranges. His remarks could be considered another example of the differences between nationalities as mentioned in a previous article above. Having resolved these issues to his own satisfaction, the game designer may proceed to develop tables of fire effect-by-range span for fronts widths'-worth or "batteries" of mixed gun types by calculating a weighted average effect for each span. Recurring to the example involving 24- and 3-pounder guns used at the beginning of this section, a simplified table of fire effect for a mixed battery thereof, equally weighted between the two types - that, is with eight 3-pounders for every one 24-pounder - might appear as follows:

Short Range 48 (= 32/2 plus 64/2)
Long Range 16 (= 32/2) Total 64

The foregoing discussion supposes kinetic energy, which increases with the square of velocity, to be the relevant gauge of smashing power. It should be noted that some experts might favour the use of momentum, which varies with simple velocity. Obviously, this would increase the relative importance of the total mass of the cannonballs. In the example comparing equal front widths' worth of 3-pounder to 24-pounder guns of like design family, such a substitution of momentum for kinetic energy as the measure of smashing power would result in the 3-pounders delivering not double but quadruple the aggregate smashing power per unit time over their range half-as-long, thus:

Range	24-pdr	3-pdr
Short	16	64
Long	16	0
Total	32	64

Clearly, this also abolishes the equality (obtained using kinetic energy) among equal front widths'-worth of different artillery types in cumulative smashing power delivered upon a steadily approaching enemy over the entirety of its advance. But since their operating costs (denominated in horses required) remain equal, this would make lighter artillery a better buy relative to heavier. The continued inclusion of heavier types among the field batteries would therefore depend upon their long-range capability per se being valued much more highly than otherwise.

In summary, game designers may wish to employ the above-mentioned formulae in order to determine range and impact. The basic concept is the force applied to the projectile (kinetic energy) is determined by the amount of powder used to expel the cannon ball, and barrel length with air resistance affecting the range to which the cannon ball would reach before it first contacted the ground, if there were no intervening targets. Of note, the amount of powder had to be measured properly as there was not a consistent amount of kinetic energy produced. British velocity tables from the 1750’s indicated that a 9- pounder cannon could fire a ball at approximately 1,052 feet per second with a charge of 2.25 pounds (about one kilo); however, a charge of 6.75 pounds (three times the amount) increased the velocity by only 50%. The impact would not be 50% greater because of the increased air resistance.

There are, however, many more factors to consider. These tend to make the formulae less precise and so one can overlook them in terms of rule development. The quality of the gunpowder varied. First it was an equal ratio of the three basic ingredients: saltpetre (potassium nitrate), charcoal and sulphur. Later saltpetre was increased to make the ratio 4:1:1 and by the end of the 18th Century, it was often 6:1:1. In the 19th Century, the recipe was standardised at 75:15:10. The original gunpowder was dust or powder. The introduction of “corning” by which all the ingredients were mixed and then compressed into cakes that were cut into grains or “corns”, produced a better quality of gunpowder. Unfortunately, it was difficult to reproduce cakes with consistency so there were noticeable differences from one batch to the next. Gunpowder was produced in both coarse- and fine-grained types. Depending on which type was used, the amount in a charge varied with more of the later required per charge.

For example, fine-grained powder may equal the weight of the projectile, while only 75% of coarse-grained powder was needed.

Powder needed to be kept dry and protected from sparks or flames. Gunpowder will absorb moisture from the air so humidity became an important factor even if there was no exposure to rain, snow or water.

In an effort to standardise the quantity of powder per charge, equal amounts were stored in cartridges. These were made of paper, canvas, linen, parchment, flannel, wood and silk. Their drawback was limited destruction when a cannon was fired. The residue (and loose powder) fouled the barrel, which then had to be cleaned otherwise the next projectile could not be loaded and the touchhole became blocked.

The quality of the metal used to produce barrels, and barrel length and bore were also factors in determining the initial velocity. A long barrel of good quality metal was better at containing the explosion and ensuring the consumption of powder and cartridge. The bore needed to be “tight” so that the projectile fit snugly so that only a minimal amount of the energy escaped around the projectile down the barrel. Metal fatigue did eventually render the gun inoperable, sometimes very suddenly and deadly during repetitive firing. There was the priming vent to consider. Fine-grained powder was poured into the vent after the gunner had pricked the casing of the cartridge. This was then ignited and in turn set off the gunpowder charge. The gunner had to expose the powder of the cartridge when pricking, and then pour sufficient powder into the vent in order to fire the cannon properly. If the vent was clogged or the cartridge not opened, then the cannon could misfire.

The gun crewman who cleared the barrel between rounds had to “clean” the barrel of residue and quench any sparks to prevent premature explosions and clogging. So without saying more, it is obvious that many things could alter kinetic energy and rate of fire. The experience and actions of the gun crew often determined how well a cannon performed. The only statistics that can really determine the influence of artillery are not normally recorded. The true measure of the worth of artillery fire is based on number of guns firing, number of rounds fired, and the length of time spent firing. To these numbers can be added the casualties inflicted by the artillery fire. Often, a cannonade produced a greater psychological than physical effect in battle. One example of limited impact is the Battle of Valmy during which there was a great expenditure of munitions with minimal impact.