Paul Koch used to use the above salutation to end his letters. I'm not sure if he's still using it, but it always seemed sort of silly to me... I don't necessarily want my dice throws to be high every time, there are occasions on which I want them low.
All of which is an introduction to a discussion of dice tossing. In most of the rules systems I generate, combat system results are a function of three parameters:
- H The number of casualties you inflict on the enemy. Depending upon the rules, it could be a count of hit markers, or stands wiped out, or figures eliminated, etc.
It's just a general indication of how effective you are in your impact on the enemy force.
N The number of your remaining forces. This can be a count of your remaining stands, or figures, or how many boxes you've still got on your data sheet. This is an indication of how effective you are in keeping your troops alive.
D A random die roll... most of the time, I use a 10-sided die.
The three parameters are then combined in a general "efficiency equation" and the winner of the combat is the side with the higher efficiency factor:
- Efficiency Factor = (H + N) x D
The first term in the calculation, (H + N), can be regarded as an indication of your "general effectiveness", GE. Which now gives rise to the question: if Side A has a GE of so many points, and Side B has so many, what should the probability be of Side A coming out on top?
For example, suppose that in melee, you came out with a GE of 9, and your opponent scored a GE of 3. You're three times as effective as he is, but what's the probability of your winning the fight? Obviously, with your 3-to-1 advantage, it shouldn't be a 50-50 outcome, and, just as obvious, you shouldn't have a pure 100 percent chance of winning. Choosing the answer, which lies somewhere between 50 and 100 percent, is a highly subjective exercise.
An interesting place to start is the published boardgame. If one examines the typical Combat Results Table as used in many boardgames, the side with a 3-to-1 advantage usually has a 66% chance of winning. The table will state that the attacker will toss a 6-sided die, and with a die toss of 1,2,3 or 4, the outclassed defender will be pushed back, or eliminated.
The table indicates that only with a toss of 5 or 6 (33%), will the defender prevail.
With a 4-to-1 ratio, the Combat Results Table states that a toss of 1,2,3,4 or 5 gives the advantaged side a win (83%). Correspondingly, if the ratio is 5-to-1 or higher, any toss of the 6-sided die produces a win, i.e, all the results are labeled "defender pushed back" or "defender eliminated". In effect, the table says you just can't lose.
The Simon system has both parties tossing a die... not just the attacker. And the Simon system also says that each side will multiply its points by its die roll. It turns out that with Side A given a 3-to-1 advantage, then when A multiplies his toss by 3, and B multiplies his toss by 1, Side A has an 87.6% (round up to 88%) chance of winning.
Question: in the 3-to-1 attack, is 66 percent a "better" number than 88 percent?
Here's a brief comparison of the difference in results, giving the percentage chance that the larger force (Side A) will win:
| A/B Ratio | Boardgame Combat Results Table | Each Side Tossing a 10-Sided Die |
|---|---|---|
| 2:1 | 50% | 79% |
| 3:1 | 66% | 88% |
| 4:1 | 83% | 92% |
| 5:1 | 100% | 95% |
Note that if you attack at a 2-to-1 advantage, the boardgame table gives you no advantage at all... each side has an equal chance of winning. In contrast, the 10-sided-die results give a fairly good shot at victory with a 79 percent.
Recently, a visitor to the Simon household, newly arrived from the British Isles, Professor Thomas J. Elsworth of the environs of oxford, distinguished member of the Centre For Provocative Wargaming Analysis, took issue with the results using the 10-side die. He said the percentages seemed a little too high. Perhaps, he went on, instead of using a single die roll as the multiplier, each participant could toss two 10-sided dice, and take the difference as the multiplier.
My curiosity was piqued, and I dashed to my computer, and had it perform a series of calculations taking two 10-sided dice and using the difference as the multiplier. The results are given in Table #2 on the next page.
But again, the question arises: which set of results is "better"?
| A/B Ratio | Boardgame Combat Results Table | Multiply by: | |
|---|---|---|---|
| Each Side Tossing a 10-Sided Die | Difference of 2 Dice | ||
| 2:1 | 50% | 79% | 72% |
| 3:1 | 66% | 88% | 80% |
| 4:1 | 83% | 92% | 85% |
| 5:1 | 100% | 95% | 87% |
I also ran out the numbers resulting from using a 6-sided die, both a single die as a multiplier, and the difference of two dice as a multiplier. There wasn't too much difference in the results obtained from the 10-sided or the 6-sided die.
Having looked at the use of dice as multipliers to each side's effectiveness, I then looked at the dice when used in an additive manner. Way, way back in the June, 1985 REVIEW, I published the following with reference to THE SWORD AND THE FLAME, which has both sides add factors to their 6-sided die rolls:
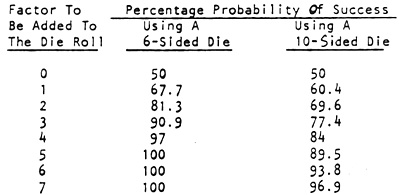At right, the following table indicates the probability of success in winning a combat if the combat factor is added to the die roll:
Thus the British trooper fighting the Zulu with a +1 advantage has a 61.7% chance of winning. Note that with a 4 point advantage, the melee is pretty one-way, regardless of the type of dice used.
One thing should be noted from the above table. Using additive factors, it's impossible to tell the force ratio being considered, i.e., by adding factors, there's no way of specifically indicating a 3-to-1 or a 2-to-1 advantage.
One simply says: "H-m-m... since Side A has a lot more men in the combat than Side B, I think I'll give Side A a +2 modifier and hope for the best."
Now, have I reached any conclusions as a result of all the above? The answer is... I shall stick to use of the single 10-sided die as a multiplier. I can't say that the results obtained are "better" than the other methods, but at least it's quick and efficient.
Back to PW Review July/August 1993 Table of Contents
Back to PW Review List of Issues
Back to MagWeb Master Magazine List
© Copyright 1993 Wally Simon
This article appears in MagWeb.com (Magazine Web) on the Internet World Wide Web.
Other articles from military history and related magazines are available at http://www.magweb.com