In an article, some years ago, I set forth what I termed a "victory point equation", designed to enable participants in a battle to judge how decisive the battle results were. It looked at force and loss ratios, threw in a "survivability ratio" factor, and combined the three into one final numerical outcome. It was picked up, in part, by George McCoy's WARGAMER'S DIGEST way back in the 1970's, in which it was used in several of the scenarios presented in that magazine to assess victory. Unfortunately, the wargaming world, as a whole, was not ready for this concept; it was derisively termed another one of Weird Wally's Warped Wonders. The Lion of Ostlandt, both on and off the table, is not one to be held down for long... at least, for no more than a decade or so... and so I'm back with yet another variation in the victory point formula. Permit me to 'splain... We look at a one-sided battle: Side A with 4 units, versus Side B with 10 units. Assume the battle results are: A ... Out of 4 units, he loses 2 units, has 2 remaining B ... Out of 10 units, he loses 5 units, has 5 remaining Each suffers a 50 percent loss, or casualty, ratio. obviously, however, A's ratio is a "better" one, since with only 4 units, he battered a much larger force. Indeed, Side A caused B to lose more units than A started with! All of which says that the simple loss ratio of 50 percent for each side doesn't really tell you anything... it Is got to be modified to account for other factors. After playing around with the numbers, what I did was to generate a simple equation for each side in which all the "good things" were in the numerator - acting as multipliers - and all the "bad things" were in the denominator - acting as divisors. A listing of these good and bad factors for Side A is: Good B Side B's force size BL Side B's losses AS Side A's survivors Bad A Side A's force size AL Side A's losses Note that as part of Side A's "good things", we list the size OfB's force. The bigger B is, the harder he falls, sez Side A, who wants full glory for besting a large enemy force. And so, for Side A, the Victory Point (VP) equation becomes: A's VP =B/A * BL * AS Side B has a similar equation, i.e., force ratio, enemy losses, own survivors, etc. Note first that in the first factor of Side A's VP computation, the size of the opposing force, B, acts as a multiplier... in other words, Side A gets credit for taking on a superior force. In similar fashion, A's own force size acts as a divisor... which is another way of saying that the bigger A's own force is, the less the credit he receives. Second, in the second factor, A gets credit for B's losses, for knocking off B's men, i.e., the greater BL, the higher A's VP. Third, the third factor gives Side A credit for having a survivor or two... if he's wiped out, AS equals zero, and A gets no victory points at all. And note also that the above deals only with the numbers of units involved; it takes no account of other items which might impact on the decision as to who actually achieved a victory in combat, items such as the taking and holding of geographical objectives. If the equation is used in the example I first gave, the battle in which Side A was outnumbered 10-to-4, and in which both forces were knocked down to 50 percent of their initial values, the numbers are: Example 1 B B's force (10) BL B's losses (5) BS B's survivors (5) VP for Side A = 25 A A's force (4) AL A's losses (2) AS A's survivors (2) VP for Side B = 4 As far as the above numbers go, therefore, Side A definitely had the better of the deal. The VP ratio of 25:4 comes out to 6.25. Let's check a fairly even battle; Side A has 10 men, and B has 10 at the outset. The results are given below: Example 2 B B's force (10) BL B's losses (3) BS B's survivors (7) VP for Side A = 24 A A's force (10) AL A's losses (2) AS A's survivors (8) VP for Side B = 14 The VP ratio of 24:14 comes out to 1.71. This VP Factor of 1.71 may seem high, however, it's not as significant as it would first appear. By playing with the numbers, substituting different force sizes and loss values, and examining the resultant figures, it turns out that a "significant victory" occurs when the VP Factor is around 6 or larger. 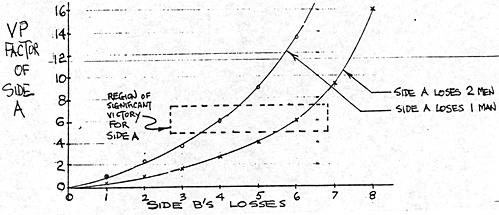The graph shows the trend of the VP Factor as losses on one side go up. What I did was to take two equal forces, both of which had initial strength 10, and assumed, for the first curve, that Side A always lost I man, and compared this with different numbers of casualties of Side B. Then, for the second curve, I assumed that Side A always lost 2 men, and compared this with different losses of Side B. In the region wherein the VP Factor of Side A to Side B is 6, B's losses are about three times that of Als. The region wherein the ratio is 8 or more repr esents total defeat for Side B... his losses amount to a wipeout. Few wargames should result in a VP Factor entering the 118 or more" region. Most table-top battles, will result in a VP Factor around 2 or 3, similar to the results set out in Example 2, above. Casualty differences between the two sides usually won't vary more than 10 or 20 percent. What this means is that if one sets a value on a particular terrain objective, a town or hill for instance, of 3 points, then this, in effect, gives the geographical objective the equivalency of a VP Factor of 3. Add this to the VP Factor resulting from casualties during the. battle as defined above, and one can come up with a total VP Factor. Thus in Example 2, Side A, from its casualty VP Factor of 1.71, can it only be said to have won a rather insignificant victory. But if it captured a town worth 3 points, the total VP Factor of 4.71 brings it that much closer to a significant victory. Back to PW Review February 1992 Table of Contents Back to PW Review List of Issues Back to MagWeb Master Magazine List © Copyright 1992 Wally Simon This article appears in MagWeb.com (Magazine Web) on the Internet World Wide Web. Other articles from military history and related magazines are available at http://www.magweb.com