Richard Berg used the phrase "random chaos" to describe the effect of the OCS surprise rule in his review of Tunisia. He may have meant to characterize OCS combat resolution as wildly unpredictable, and I agree that the outcomes of individual combat resolutions are more difficult to predict than in many games with odds-based combat results tables (CRTs). But the paradox of randomness is that the greater the number of random events, the more clearly a pattern emerges, the pattern implied by the probabilities of the different outcomes. Evolution works and casinos make money because of the large scale predictability of random events.

An OCS scenario or, more so, campaign game, includes enough surprise and combat resolution dice rolls for the patterns implied in the units' action ratings (ARs) to become manifest. Players who cooperate with these patterns tend to win more combats, in the long run, than players who ignore or play contrary to the patterns. In this way, the OCS action rating and surprise rules encourage players to use historically plausible combat doctrine. Basically, talented units are better in all situations but especially good in mobile combat. Poor AR units are best used en masse and tend to do better if bolstered by fortifications, supporting artillery, and talented cadres.

The preceding two sentences state OCS truisms. The rest of this article looks at the (rather easy) math behind them and the tactical implications of that math.

First a quick review of how dice work. Skip ahead if you know this material, which applies to any game that uses two standard dice to generate results from 2 to 12. While the roll of a single die or of a pair of dice read as an 11-66 result produces a linear probability "curve," multiple dice summed give a normal distribution, similar to the classic bell curve.

Figure I - The probabilities of "making - that is rolling equal to or higher than - a number as approximate percentages. The gradient in not linear. The change in probability from one pip to the next is greatest near the middle of the range, centered on 7.

For two six sided dice, the curve peaks at 7. In cases when a player is trying to "make" a number (roll that number or greater), the probability curve looks like half a bell curve (see Figure 1). The same goes for attempts to roll no higher than a number, but with the curve flipped to its mirror image.

The numbers show that the difference of a single pip is a larger swing in probability near the center of the bell curve than near the extremes. For example, making a 6 is 16% easier than making a 7, while making a 10 is only 9% easier than making an 11. Also, while rolling an 11 is twice as likely as rolling a 12, making an 11 (i.e. 11 or higher) is three times as easy as making a 12. If someone asks you what number is most likely to come up on a two-dice roll, answer "seven"; if someone asks you whether a two-dice roll is more likely to come up 7 or some other number, answer "some other number." If someone asks whether the roll is likely to make a 7 or better, answer "yeah, slightly more likely than not."

So much for the 2-12 roll in general. Let's look at OCS surprise rolls:

Surpriser	Overrun	Regular Combat
Attacker wins surprise:	9 or more	10 or more
Defender wins surprise:	6 or less	5 or less

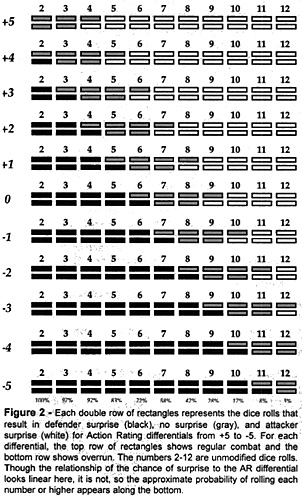
The action rating differential (attacker's AR - defender's AR), which may be positive or negative, is a modifier to the surprise roll. The attacker has to make a 10 in regular combat to win surprise. If the action rating differential is 0, the probability of attacker surprise is 17%. With an AR 2 greater than the defender's, the attacker must make an 8 (modified to 10) to win surprise, and the probability of doing so more than doubles, to 42%. In an overrun, the attacker's probabilities of winning surprise are 28% at even ARs and a whopping 58% at a +2 AR differential (See Figure 2).

In any situation where the attacker and defender have equal action ratings, the chances of attacker and defender surprise are not even-, rather, the defender is more likely to win surprise. in regular combat, the defender's chance of surprise is 28%, while the probability of attacker surprise is only 17%. In an overrun, the probabilities of defender and attacker surprise are, respectively, 42% and 28%. Surprise rolls with a zero AR differential are not "fair"; they favor the defender.

The tactical lesson so far is that if you want the combat strengths of the units involved to have the greatest influence on the combat resolution, then attack in regular combat, not overrun. Likewise, if you have good numerical superiority in terms of overall combat strength points, attack in regular combat unless you have a good AR differential. Conversely, if you want talent to have more influence, then you should use overruns.

The terrain rows on the Combat Table also relate to the action ratings of the units involved in a combat. The difference between one column and the next requires a greater difference in combat strengths in more restricted, defender friendly terrain. For example, in Open the next higher column from 3:1 is 4:1, an addition of attacker strength points equal to the defender's strength. To achieve the same column shift in Close means jumping from 4:1 to 6:1, an addition of two times the defender's strength. In Very Close it's 6:1 up to 9:1 (three times the defender's strength), and in Extremely Close it's 12:1 to 16:1, quadruple the defender's strength. So the tighter the terrain, the less weight of numbers counts for achieving better Combat Table columns. But the surprise roll applies one to six column shifts regardless of the terrain row. Therefore in combats between the same units, the tighter the terrain, the more important the surprise roll is.

But how important is the surprise roll?

Some people assume that the shifts (up to six columns either way!) tend to change results drastically from what they would otherwise be. Sometimes the effect is drastic, but it's usually rather modest. In the long run, combats with surprise results will shift three columns left or right. Given the expected value of 3.5 for the average of a series of surprise column shift rolls, lets conservatively say three shifts is typical.

Let's take a mediocre attack, 3:1 in Open, when the attacking and defending lead units have equal ARs. Without surprise the most likely result, on a roll of 7, is Aol/Dol. With defender surprise of three columns left, the same dice roll yields ALlol/Dol; if the attacker wins a three column surprise the result would beAol/DLlol. The difference here is important, but not overwhelmingly so. What's the worst that could happen?

Figure 2 - Each double row of rectangles represents the dice rolls that result in defender surprise (black), no surprise (gray), and attacker surprise (white) for Action Rating differentials from +5 to -5. For each differential, the top row of rectangles shows regular combat and the bottom row shows overrun. The numbers 2-12 are unmodified dice rolls. Though the relationship of the chance of surprise to the AR differential looks linear here, it is not, so the approximate probability of rolling each number or higher appears along the bottom.

A six column defender surprise and snake eyes on the combat roll gives AL2, while maximum attacker surprise and boxcars yields Ae3/DL2o2DG. Now those are extreme, but so are the dice rolls.

The possible results are not equally likely along this range. When the units in this example have equal ARs, the probability of defender surprise is 28% for regular combat and 42% in overrun. The probabilities of attacker surprise are, respectively, 17% and 28%. So a 3:1 combat between equally talented troops tends to favor the defender.

Now let's modify this example to look at the same combat with an AR differential of +3, a strong advantage for the attacker. The range of outcomes on the Combat Table is the same as it was before, since Action Ratings never affect the number of column shifts, only the chances of those shifts occurring. Now the probability of defender surprise drops to 3% for regular combat and 8% in overrun, while the probability of attacker surprise rises to 58% in regular combat and 72% in overrun. But wait, it gets better.

Since the AR differential is also a dice roll modifier on the Combat Table, an average dice result is modified to a 10, yielding Aol/Dol in case of a three column shift defender surprise and Ae4/DL1 o2 in case of a three column shift attacker surprise. Thank you, bell u .

How about a real life example, from one of my recent Guderian's Blitzkrieg II (GBII) contests. Gary Perkins wanted to send a single-step 5-5-8 (combat strength, action rating, movement allowance) assault gun battalion against one of my full strength 11-1-1 rifle divisions, which have two steps.

He wondered, "What happens if I overrun here?" I replied, "You risk losing the panzers, but you have a good chance of hurting me. You might even vaporize the whole division." In Open terrain tank type units have their combat strengths doubled, so the initial odds were 1:1. On this column the attacker needs to roll a 9 or better to avoid death (complete failure for a single step attack); with the +4 dice roll modifier, though, that minimum roll drops to a 5, pretty easy to make at 83%. A roll of 7 (average luck) will inflict a step loss on the defender even if the attacker retreats, and boxcars doesn't do all that much more damage.

But now consider surprise. The probability of defender surprise is a mere 3%, while the probability of attacker surprise is 83%. With average dice, the attacker will achieve surprise, shift the odds three columns right, and roll an adjusted 11, inflicting Ae4/DLlo2.

By rolling a raw 9, adjusted to 13, on this column, the assault guns kill the infantry outright. Gary wiped out the division, but imagine it had survived and staggered back a hex or two and become DG. A unit that has suffered at least 50% casualties has its combat strength halved, while the DG halves that strength again and reduces the AR by one. In that case the shot up division would have had a current combat strength of 2.75 and an effective AR of zero, making it easy prey for, say, an overrunning motorcycle battalion.

What if you don't have talented troops and even have to attack at a negative AR differential?

It can be done, but it takes high combat strength. Consider that 3:1 attack in the Open at a -1 AR differential, not uncommon for Soviets attacking Germans in GBII or Enemy at the Gates (EatG). In this case the typical defender surprise of three shifts, along with a modified combat dice roll of 6 yields ALlol/Dol. If you'd rather inflict an Ao1/DL1o1 with the same dice, you need to pump the initial combat odds up to 11:1. The defender's probability of surprising you in this situation is 42% in regular combat or 58% in overrun. You do want to boost the odds, either by attacking with more units or by inflicting a DG on the defender.

Of these two possibilities, adding troops costs more combat supply, but so does firing a barrage. Inflicting a DG has the advantage of reducing the defender's AR by one. Attacking with more steps can also help you afford to take any option as a step loss and so prevent the defender from ignoring any options you inflict. To achieve either a preliminary DG or high combat odds, you will do better by attacking in the Combat Phase rather than in an overrun. But given the probability of defender surprise, you don't want to overrun anyway.

Massing your troops and waiting till the Combat Phase to make up for a relatively poor AR brings the risk that your opponent may use the Reaction Phase to reinforce the defending hex or disorganize one or more attacking stacks with barrages. Large stacks of attackers are especially vulnerable to air and artillery bombardment because of the density modifier. Oh well: welcome to the OCS, where even your small scale choices involve various, sometimes difficult, trade-offs. Except when you're attacking units in Strategic Move Mode, there are no "no brainer" combat decisions.

General Guidelines

That said, there are some general guidelines that the rules for surprise, overrun, and regular combat imply. The effects of the AR differential on surprise (see Figure 2) and combat resolution underlie these guidelines which, while they won't always protect you from disaster, will prove reliable in the long run:

• A high AR is a good thing in combat, and "high" means better than the opponent's. A unit with a 3 fighting a unit with a 1 (or a 2 and a DG) is every bit as elite as a unit with a 5 against a unit with a 3. You don't always know what the other guy's AR is, but you can often make a good guess.
• An AR advantage is especially helpful in overruns and in difficult terrain. In an overrun surprise is more likely, and in tighter terrain surprise is more helpful to the side achieving it.
• Remember the bell curve. The difference of one pip can mean a fairly big shift in probability toward the middle (where you need to make rolls of 6, 7, and 8). Defending in a hedgehog and fighting a DG marked enemy are ways to earn a pip on the surprise roll. At the ends of the bell curve, gaining a pip to boost the probability of attacker surprise from 3% to 8% or from 92% to 97% is less cost-effective. Spending supply on a barrage for the sake of such small increases is probably more wasteful than spending it to add more units to the attack.
• If you don't have the AR advantage, or even if your AR is equal to the enemy's, look for ways to compensate, including adding more combat strength to the combat, defending in a hedgehog, and weakening the enemy's combat strength and AR with a DG (Disorganized) result.

The broader corollary of these guidelines is that if your army is more talented than the enemy's, you will tend to do well in mobile situations where you make your lower odds attacks as overruns and avoid forming large attacking stacks for your opponent to disorganize in the Reaction Phase. If your troops are less talented, you will prefer to fight set piece actions in the Combat Phase and try to maximize the effects of weight of numbers and supporting artillery and air power.

That's what the numbers say

Then there's the psychological effect of having lots of elite troops, like the Germans in pretty much every OCS game where they appear but especially in Guderian's Blitzkrieg 11 and Enemy at the Gates. In these games, the sense of having "godlike fives" may inspire the German player to be hype r-agg ress ive, while the Soviet player will look at his talentless peasants and seek safety in numbers. Remember, though, that the AR differential, not the AR itself, is what makes the difference. Those AR 5 crack German troops aren't quite so dominant against, say, the Allies in Sicily, who have a good number of AR 4 and even AR 5 units and few with an AR less than 3. Sure, attitude matters, but so does math.

What may look like "random chaos" in two, three, or a dozen individual combats adds up to a pattern over the course of an entire game. The probabilities in the surprise and combat dice rolls are the basis of this pattern and the reason you should learn to use your units in ways that emphasize their strengths and compensate for their deficiencies. This article doesn't touch on important points like how mode, action rating, and available supply determine a unit's combat potential or the importance of the special combat strength modifiers for combined arms tactics. But a close look at how the surprise and combat dice rolls work should improve your play. I neither expect nor want people to be pulling out this article during play to try to calculate each combat to the last pip.

I do hope that this analysis helps you make decisions with a clearer understanding of how combat strength and action rating bullets and brains - interact to affect combat results.