This report presents the changes to the gunnery rules which are included in the second edition of Command at Sea. The changes described were in response to the following problems found in the original system:
- The chance of a hit in each range band was too high.
- Shell damage was far too high, especially in the Short and Medium range bands.
- Damage by gun mount was unrealistic. Combined with high individual shell damage, total damage per Turn became incredibly high.
- The original range Bands resulted in immunity zones that allowed ships to get far too dose before belt armor penetration occurred.
- Armor penetration values had to be reanalyzed as some battleships had deck armor ratings that could not be penetrated at Extreme range.
All of these problems were identified by players. Each one will be dealt with in detail in this article. Some of them were resolved by reexamination of the model's basic assumptions. Others were answered by new information and documents that became available after the first edition was printed. These rules modifications are based more on analytical results instead of subjective estimates and thus, provide a better fit to historical World War II battle experiences. All assumptions made in developing the models will be clearly stated so that the players will know what they are and how they affect the model's output.
1) Range Band Probability of Hit Analysis
During scenarios played at Historicon '94, it became apparent that at Short and Medium range bands too many hits were occurring. Annex J showed that the short range P h of a single shell was given as 0.24. While this value is small in comparison to modern weapon systems, it appeared to be too high for the era which CaS tries to simulate. Unfortunately, there are very few engagements where a good account is kept of how many shells hit compared to how many were fired. The following engagement list is an overview solely from the Dulin and Garzke battleship series. Limited official Navy sources and the recent World War II in the Pacific Conference lectures all tend to confirm what was found in the battleship books.
a) Case Studies
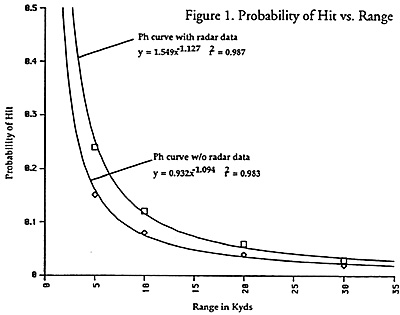Six case studies, all battleship engagements, were studied do derive historical P h 's. These were Massachusetts vs. Jean Bart, Washington vs. Kirishima, Richelieu vs. Barham, Prince of Wales vs. Bismarck, Rodney and Duke of York vs. Scharnhorst. All these engagements are well-documented, with the firing range, duration, number of shots, and number of hits all available.
The data from these cases, for the most part, are pretty much in agreement with the original CaS P h' s of 0.24, 0.12, 0.06, and 0.03 tor the tour range bands. The problem that arises from this, however, is that the specific cases above are for radar directed gunnery. A good check for this hypothesis is to compare the Rodney vs Bismarck case with the following curve based (Figure 1) on the Ph's specified above. If the range of 4 kyds is put into the Ph curve with radar data the Ph is calculated to be about 0.33 which is very close to the historical data. This tends to support the assertion that the original Ph's Include radar direction. Since the shape of the probability of hit curve is consistent with numerous sources, including a paper study on battleship accuracy which includes various spotting techniques, it is assumed that gunnery with optical direction only is about 70% as accurate. Given this assumption a second curve is derived that removes the radar enhancement from the base P h values. The revised Ph's are now 0. 16, 0.08, 0.04, and 0.02 for the four range bands. As one can see, the most significant changes occur at the Short and Medium range bands which supports the observations at Historicon '94.
Another factor that made the Tactical Turn range band Ph's high was the high number of shells fired per turn. This high number was due to the assumptions that sustained rate of fire was the same as maximum rate of fire and that the average turret had three barrels. First, there is a large data base of naval gunnery and army artillery analyses which shows that maximum rate of fire can only be sustained for a very short period of time. Thus, sustained rate of fire is always lower than the maximum rate of fire. For example, the USS Washington fired 75 16inch rounds in seven minutes. This gives a firing rate of 10.7 rounds/minute. If all three turrets were used, this leads to a barrel rate of fire of 1.2 rounds/minute. If only the forward turrets were fired, the barrel rate of fire is about 1.78 rounds/minute. The maximum rate of fire for this gun type is 2 rounds/ minute. The average of the two cases is 1.5 rounds/minute which is 25% below the maximum firing rate and is not an unreasonable assumption for a sustained rate of fire of power assisted naval guns.
Second, the average gun turret in World War II was a twin mount, not a triple mount. The extra barrel Increases the number of shells arriving in the target's area by 50%. Such an increase will most assuredly affect any P h calculation significantly Between these two assumptions, there is a factor of two increase in the number of shells fired in each Tactical Turn.
2) Gunnery Damage Analysis
This was an issue with many players as ships at short range were literally being vaporized in one or two Tactical Turns. While this may be historically accurate in that a ship dies quickly in a short range gunnery duet, it became obvious that they were dying for the wrong reasons. In addition, the damage model didn't seem to take into account higher muzzle velocities; a point which would greatly affect German and Italian gun systems. This ultimately lead to a review of how damage was calculated for guns in general. The best, and almost Only, historical case that could serve as a basis to work from was the Washington and Kirishima duel in which the latter was sunk almost entirely by the former. Numerous sources, however, claim the South Dakota managed to get one hit and I'll include this hit in the analysis.
a) Individual Shell Damage
The best way to start the analysis is to look at the damage done by a single shell. Only after this is completed can a larger salvo-based system be constructed. To begin with, let's look at the damage inflicted on Kirishima by ten 16-inch hits in the Second Battle of Guadalcanal. The Kongo class has 652 damage points. Assume that Kirishima suffered 85% damage from the 10 hits. This is about half way (actual average is 82.5%) between major damage (75%) and DIW (90%), and is what I consider to be a completely nonfunctional ship.
- 10X = (0.85 x 652) = 554, = X = 55 damage points/hit
From this equation, a constant was derived which would translate shell weight into damage points.
- Constant = 1225 kg/55 = 22.3 or about 22. This is not too far from the value of 20 used in Annex J.
Now we'll look at the energy content of a shell on impact. From this we can check on the accuracy of the weight constant derived above. Since the WashingronlKirishima engagement took place at 8.4 kyds (Medium range for a 16in/45 gun), the shell impact velocity for a 16 in/45 gun is close to 579 m/sec.
- Damage per shell = Constant x Total Energy
- Damage = Constant x (Explosive Energy + Kinetic Energy)
- Explosive Energy = Explosive Filler Mass x Heat of Explosion
- Explosive Energy = 18.36 kg x 4300 kj/kg (Heat of Explosion for a typical shell explosive, less than TNT)
- Explosive Energy = 78,948 kj
- Kinetic Energy = 1/2 x (Shell Mass x Impact Velociry2)
- Kinetic Energy = 1/2 x( 1224.7 kg x 579 m/sec2)/l 000 = 205,285 kj
- Total Energy = 78,948 + 205,285 = 284, 233 kj
- 55 DPs = Constant x 284,233 W
- Constant = 5,168 kJ/DP
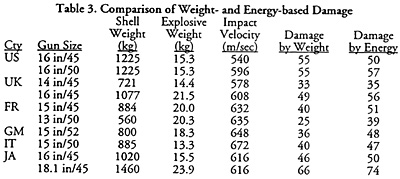A comparison of the results of the two methods is provided in Table 3 for several large-caliber guns. To keep everything consistent, the damage is for the Medium range band for each gun type. It is interesting to note that the weight-based methodology damage is always lower than the energy-based methodology and in the case of guns With very high muzzle velocities, it is off by as much as 33%. These results would seem to be at cross-purposes to the goal of reduce overall gunnery damage. But when the individual shell damage between the weight and energy methods turned out to be relatively close, in most cases, this proved that the problem lay elsewhere in the original gunnery model. A benefit of the energy methodology, however, is that an accurate damage reduction with range is easy to develop as the only changing parameter is the striking velocity of the shell.
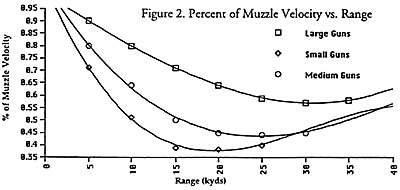The graph in Figure 2 illustrates how velocity drop-off varies with the size of the shell.
To simplify the damage calculations, a fixed set of velocity drop off values were taken off of the curves. These velocity coefficients were then used to determine the kinetic energy of the shell for the various range bands. Unfortunately, this system does not lend itself to a quick and easy procedure that could be included in Annex J. Each gun system has to be analyzed individually for each range band and each shell type to come up with the kinetic energy the shell possesses at impact Table 4 provides the % of Muzzle Velocity remaining when the shell strikes the target for each of the range bands and gun size groupings.
b) Energy-Based Damage Calculations
To use the energy-based damage system the following data for a particular gun must be known:
- Shell Mass (kg)
- Explosive loading (kg)
- Muzzle velocity (m/sec)
If shell's explosive loading is unknown, use the following weight percentage of the shell's total mass as a first order approximation.
- AP Shell: 1.5% of total shell weight
SAP/Special COM: 3.5% of shell total weight
COM: 5.5% of shell total weight
HC/HE: 8.5% of shell total weight
| Table 4. Velocity Coefficients (% Muzzle Velocity) | ||||
|---|---|---|---|---|
| Range | 18-14 in | 13-11 in | 10-7 in | 6 in. and less |
| Short | .96 | .94 | .92 | .92 |
| Medium | .79 | .73 | .66 | .64 |
| Long | .63 | .55 | .47 | .45 |
| Extreme | .57 | .50 | .44 | .42 |
Explosive energy is calculated by multiplying the weight of the explosive filler in kg's by the Heat of Explosion of the explosive. For the purposes of this model, the Heat of Explosion for all shell fillers is assumed to be 4,300 kJ/kg. The explosive energy of the shell will be the same in all range bands.
Kinetic energy is calculated for each range band as it will decrease with range as the shell slows down. The striking velocity as a % of the muzzle velocity can be determined from the velocity coefficients listed above. Multiply the muzzle velocity by the appropriate velocity coefficient for the particular gun size and range band. Next, determine the kinetic energy of the shell with the following equation:
- KE = 1/2 x (Shell Mass) x (Striking Velocity) [squared]
- Note: Since the units for this equation is Joules (J), divide the result by 1,000 to get kJ.
Total energy is the sum of the explosive and kinetic energies for each of the range bands.
CaS Damage Points are calculated by dividing the total energy by 5,168 kJ/DP.
c) Gunnery Damage Equation
With the shell's basic damage now known from the energy-based calculation, the damage potential of a particular gun system can now be determined. This final step takes the individual shell damage and adjusts it for the gun's rate of fire in comparison to the reference gun used throughout this analysis (the U.S. Navy Mk6 16in/45). If a particular gun system has a higher rate of fire than the Mk6, than it is expected to obtain more hits in a Tactical Turn and thus, do more damage than that for a single shell. The reverse would also be true for a gun with a slower rate of fire.
- Gun Damage = Base Shell Damage (as determined for each shell type in each range band) x Max ROF/2
Max ROF is used because it is more readily found in research materials. All other factors, such as the reduction to sustained ROF, Tactical Turn length, and the reference ROF are distilled down into the 1/2 constant. If a gun has a ROF of 6 or more rounds per minute, halve the ROF when calculating the Long and Extreme range bands.
Constant derivation = (Max ROF x 0.75 x 3 minutes)/(6 rounds x 0.75)
- 0.75 = Constant to reduce Max ROF to Sustained ROF
- 3 minutes = Time for one Tactical Turn
- 6 rounds = Reference gun (Mk6 161n/45) which has a Max ROF of 2 rounds every minute.
- Treat Max ROF's <1.5 rds/min as being equal to 1.5 rds/min.
Example: Here's how one would use the energy-based damage system to determine the performance of the Iowa's Mk7 16in/50 gun system.
- AP Shell Weight: 1,225 kg
- Explosive Filler: 18.4 kg (about 1.5%)
- Muzzle Velocity- 762 meters/sec
1) Explosive Energy = 18.4kg x 4,300 kJ/kg = 79,120 kJ (This will be constant for all range bands)
2) Kinetic Energy = 1/2 x (1,225 kg x %Muzzle Vel2)/1000 for each range band Use Table 4 for 14 - 18 in guns to find the Velocity
Coefficients
3) Damage Points = (Explosive + Kinetic Energies)/5,168 kJ/DP
| Range Band | Striking Velocity | Kinetic Energy |
Explosive Energy | Total Energy | Damage Points |
|---|---|---|---|---|---|
| Short | 731 | 327,296 | 79,120 | 406,416 | 79 |
| Medium | 602 | 221,972 | 79,120 | 301,092 | 58 |
| Long | 480 | 141,120 | 79,120 | 220,240 | 43 |
| Extreme | 434 | 115,368 | 79,120 | 194,488 | 38 |
NOTE: Don't be disappointed if you don't reproduce the gun damage exactly. For example, the Short and Medium range damage above is one DP higher than that in Table 5. This is because for some gun systems, we had access to exact shell velocities and these were used instead of the estimate of shell velocity from Table 4 which is an average of many gun systems.
d) Comparison of Second Edition Gunnery System to the original.
| Table 5: First and Second Edition Damage Point Comparison | |||||
|---|---|---|---|---|---|
| Country | Gun System | Hit=7 Short | Hit=5 Med | Hit=2 Long | Hit=1 Extreme |
| us | Mk6 16 in/45 | 176 | 88 | 61 | 61 |
| 68 | 50 | 40 | 36 | ||
| US | Mk7 16 in/50 | 176 | 88 | 61 | 61 |
| 78 | 57 | 43 | 38 | ||
| UK | MkVII 14 in/45 | 130/78 | 65/39 | 36 | 36 |
| 47 | 35 | 27 | 24 | ||
| Japan | Type 94 18.1 in/45 | 210 | 105 | 73 | 73 |
| 74 | 56 | 41 | 36 | ||
All of this means little if it can it be boiled down to a very hard bottom line, so here it is. Table 5 is a comparison of the new gunnery damage system to the one used in the first edition CaS rules. The comparison is for AP rounds only and the new damage values are bolded.
As the table shows, there is a significant difference between the two damage models. All gun systems have significantly lower damage (on the order of 50%) than the original gunnery system.
3) Damage by Gun Mount
During the White Elephant scenario at Historicon '94, the USS Arizona and the Yamashiro engaged each other in a long range gunnery duel. After a few ranging shots, both the Arizona and Yamashiro connected, however, Yamashiro inflicted considerably more damage (204 points) than the Arizona did (136 points) even though the individual shells did the same amount of damage and both ships had the same number of barrels firing. This disparity in the damage inflicted was due to the fact that Arizona has four triple turrets while the Yamashiro has six dual turrets. This clearly showed that damage by gun mount was an unrealistic method of determining damage. This problem was somewhat correct in the errata by limiting the damage at long and extreme range to that inflicted by a single turret. Unfortunately, the problem still exists at the shorter ranges where it has been masked by the highly inflated damage in these range bands.
The easiest and most accurate way to determine the damage potential of a ship is to count how many guns it has. If you can sling more lead, you should do more damage; providing gun size doesn't change. This would also be in agreement with the Gunnery Modification Table which uses the numbers of barrels firing to yield a positive die roll modifier. Historically, one hit per turret for large caliber guns at Short and Medium range appears to be a very good number that can be defended. For longer range fire, the number of hits were halved for each range band beyond medium. Table 6 shows the number of "hits" that will occur in the four range bands as a function of the number of barrels firing.
By using this method, damage is based on the number of barrels that fire and not the number of mounts. It will also be noted that a larger number of barrels has a greater damage potential at long range. This is entirely statistical in that more shells mean more opportunities to hit. An added benefit of this approach, is that Annex C has been significantly reduced. This is because only the different gun barrels, and not the mounts, need be listed.
| Table 6 Gun Damage Multiplier Table | ||||
|---|---|---|---|---|
| No of Barrels | Short | Medium | Long | Extreme |
| 1-3 | 1 | 1 | 1 | 1 |
| 4-6 | 2 | 2 | 1 | 1 |
| 7-9 | 3 | 3 | 2 | 1 |
| 10-12 | 4 | 4 | 2 | 1 |
| 13-15 | 5 | 5 | 3 | 2 |
4) Immunity Zone Adjustments
In a recent review of CaS, it was noted that the gunnery system did not take into account the damage and armor penetration capability of high velocity guns. A quick spot check of the armor penetration model showed that not only did the system not take into account these gun systems, but that the range band set points gave immunity zones that appeared to be too close to the firing ship. A review of the Dulin and Garzke battleship series and Campbell's book on World War II naval weapons showed that all battleship guns in the game had immunity zones that were too close. This indicated an error in the range band set points as defined in the original armor penetration model.
Research into the various battles described in the Dulin and Garzke series gave only rough clues as to when a shot was point blank" or "long range". However, the breaking up of the range bands into roughly 1/3 increments still seemed to be a good assumption. Based on this and normal distribution theory, it was assumed that the Medium and Long range bands would account for 60% of a gun's range. The Short range band, from the data available, appeared to always be at ranges less than 18 to 20% of the gun's maximum range. Based on this admittedly light data set, it was assumed that the Short Range band would be for ranges: less than or equal to 15% of the maximum range. Simple subtraction indicated that the Long range band would cover the last 25%. Using these set points, the range band of the guns would be split up as shown in Table 7.
To test this new set of range band boundaries, a number of trial cases were looked at. An illustrative example would be the Iowa's Mk7 16in/50 gun against the Yamato. In the original system, the Mk7 has a Long Range band, and hence an immunity zone against modern battleships, of 14.0 to 28.1 kyds. With the new set points, the Long Range band/immunity zone gets pushed back to 19.1 to 31.7 kyds. Exploitation of recovered Shinano armor samples indicated that a Mk:7 would penetrate around 21 kyds. Dulin and Garzke, in their Axis battleship book, gives the Yamato ~ immunity zone against large caliber guns as being about 21.9 to 32.8 kyds. Finally, the armor penetration values on the Immunity Zone slide rule were consulted and the Mk7 had an immunity zone against the Yamato of 22.0 to 33.5 kyds. The other trial cases also showed that the new set points provided more reahistic immunity zones than the original values in the first edition.
| Table 7 Range Brackets | |
|---|---|
| Range Band | Range Set Bands |
| Short | 0-15% |
| Medium | 16%-45% |
| Long | 46%-75% |
| Extreme | 76%-100% |
5) Gunnery Armor Penetration Values
During the evaluation of the range band set points, it was noticed that the Yamato, North Carolina, South Dakota, and Iowa classes all had deck armor ratings that prevented penetration by any gun system in Annex C. This is, without question, a problem with both the gun penetration and armor models. In checking out the gunnery side, a review was made of the Dulin & Garzke battleship series, a series of articles in Warship International by Nathan Okun, including the armor penetration equations, and the Immunity Zone Slide rule. The results did show a distinct relationship with gun bore size which was the basis for the penetration model in the first edition rules. However, there were differences in the penetration factors between the original Annex J values and the subsequent evaluation.
| Table 8 Range Band Penetration | ||
|---|---|---|
| Shell Type | Original Penetration Factor | New Penetration Factor |
| Short | 1.7 | 1.75 |
| Medium | 1.4 | 1.35 |
| Long | 0.2 | 0.3 |
| Extreme | 0.4 | 0.55 |
| Table 9 Penetration Factors | ||
|---|---|---|
| Shell Type | Original Penetration Factor | New Penetration Factor |
| AP | 1.00 | 1.00 |
| SAP, Special COM | 0.60 | 0.60 |
| COM | 0.30 | 0.30 |
| HE, HC | 0.20 | 0.15 |
As Table 8 shows, the direct fire factors are almost identical, however, the differences in the plunging shell fire factors are as large as 30%. Using the new penetration factors, no battleship is completely immune from large caliber (16+ in) plunging shell fire at Extreme range. In addition, modifications to the armor system will also reduce deck armor values which will make 15in guns, and in most instances 141n guns, effective at Extreme range. To accommodate the higher muzzle velocity guns (any gun that is 50 calibers or greater in length), multiply the Short and Medium range penetration by 1. 12. Long and Extreme range factors are unaffected by the higher muzzle velocity as the shell is approaching terminal velocity, like an other shell, but at a longer overall range.
The shell penetration modifiers were also looked at and in both cases the results were nearly identical. In the second review, however, HC and HE shells were reduced in penetration ability based on a detailed review of shell construction which showed a larger difference in the shell wall thickness between HC/HE and Common rounds. Table 9 shows the old and new shell penetration factors.
6) Conclusion
In conclusion, there were several problems with the original gunnery system that was used in the first edition of CaS, some were minor and others major. Virtually all problems were identified by players in either letters or E-mail. The modeling changes described above appear to correct the deficiencies that were identified and will make CaS a more realistic World War II simulation.
BT
Back to The Naval Sitrep #4 Table of Contents
Back to Naval Sitrep List of Issues
Back to MagWeb Master Magazine List
© Copyright 1995 by Larry Bond and Clash of Arms.
This article appears in MagWeb (Magazine Web) on the Internet World Wide Web.
Other military history and related articles are available at http://www.magweb.com