For several years now, my home-brew Napoleonics rules have used a firing procedure which models, in rough fashion, the fire effect of that era. Two factors were predominant in the generation of the technique: a. First, a reading of the text FIREPOWER by Hughes, Scribner & Sons, 1974, which shows in graphic form (to a first order approximation) that the firepower of both musketry and artillery falls off linearly with range. In other words - as range increases, each and every distance increment is accompanied by a corresponding drop in weapon accuracy and, therefore, the number of hits on the target. 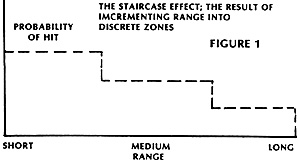b. Second, a dissatisfaction with the firing procedures of existing rules, almost all of which, for ease in calculation, divide the reach of a weapon into short, medium and long range. Thus a chart containing a list of firing modifiers might provide, for example, a "+1" for short range, no modifier for medium range, and a "-1" for long range, where the 3 ranges might be defined as 0 - 6, 6 -12, and 12 - 24 inches, respectively. The dissatisfaction stemmed from the fact that a unit at 53/, inches merits a "+1", whereas the same unit at 6 1/2, inches, having now crossed into medium range, receives no such fire increment. Indeed, the fire effect is constant until the unit passes the next threshhold and enters the long range region. These abrupt transitions between the zones, bringing with them instantaneous changes in firepower, seemed illogical. Figure 1 depicts a typical firepower plot showing the staircase curve that results from having discrete changes in the probability-of-hit (POH) as the target range varies. MUSKET FIRE A closer approximation to the dropoff in accuracy versus range is obtained by use of the curve in Figure 2; the graph shown, P(m), is for musketry. Table-top scale is 1 inch equals 10 yards; note that the musket firepower effect goes to zero at 15 inches or 150 yards. Note also that at "zero" range, P(m) is not 100% - thus at point blank range, every firing figure does not get to eliminate an opposing figure. Instead, the maximum probability is chosen to be 30% - in terms of playability, this maximum represents a good balance between actual casualty rates and that required to conduct a fast moving gameable battle. 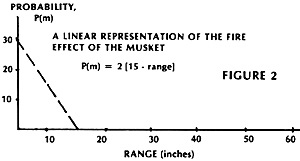The graph is used to determine the probability, P(m), for each figure firing. This is them multiplied by the number of firing figures to arrive at a final probability-of-hit (POH). For example, P(m) from the curve at a 5 inch range is 20%; if 11 figures fire, the total probability is defined as POH = 11 x 20 or 220%. This interpreted to mean 2 sure hits and a 20% chance of a third. I realize the purists are now up in arms. One should not simply total probabilities in the way I described. As an example, consider 2 figures firing, each with 30% probability of hitting the target. The way my method works, I'd add the 30's of each figure to arrive at a POH of 60, and declare that they had a 60% chance of a hit! The mathematically correct way would be to analyze the possibilities as shown below. The firing figures are denoted as Jean and Pierre. Note that the probability of either Jean or Pierre hitting is 30%, while the probability of their missing is 70%. The possible outcomes are: Possibility 1 - Jean hits (.30), and Pierre misses (.70). . .(.3) x (.7) = .21; Possibility 2 - Jean misses (.70), and Pierre hits (.30). . .(.7) x (.3) = .21; Possibility 3-Jean hits (.30), and Pierre hits (.30). . .(.3) x (.3) = .09. Probability of at least one hit by Jean and Pierre ....51. Which means a 51e chance. Thus my method of totalling percentages actually grants Jean and Pierre a higher POH than does the exact mathematical analysis, 60% to 51%. This slight increase in firepower is nonobjectionable; it makes the battle slightly more "bloody", but not significantly so. Indeed, despite the higher probability of their becoming casualties, neither Jean nor Pierre have ever complained of unfairness or mistreatment . . . even as they were borne from the battlefield, stout lads. The curve of Figure 2 is represented by the equation: P(m) = 2 (15 - range) The range value can, after measurement, quickly be popped into the equation and the appropriate probabilty determined. If the figures in a unit are not all equally distant from the target, i.e., each man firing at a range slightly different from that of his neighbor, the average range is used for the entire unit -there is no need to measure every individual figure range to the target. Thus if we measure, in our 10 man unit, that Jean, the furthest man, is 11 inches from the target, while Pierre, the closest man, is 5 inches, the calculation becomes: RIFLE FIRE Using the linear musket fire relationship as a base, rifle fire, or P(r), may be defined as: P(r) = 30 - range Figure 3 compares the musket and rifle fire curves. Note that at "zero" range, both reach the 30% mark, and that the maximum rifle range is 30 inches, or 300 yards, double that of the musket. I use the term "zero" in quotes, because even when the measured range is zero and the opposing figures are nose-to-nose, the table-top scale is distorted to the extent that the actual range at which point blank fire takes place is probably on the order of 8 to 12 yards. 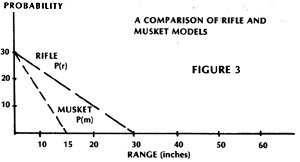The curves of Figure 3 indicate that, at very close range, there is not much difference between rifle and musket fire effect. For example, at 3 inches (30 yards): For the musket, P(M) = 2 (15 - 3) =24% For the rifle, P(r) = 30- 3 = 27% The difference increases rapidly, however, as the firing units move further apart, with the musket effect falling to zero at 15 inches, at which point the rifle fire effect is still appreciable. Before we go further, I should point out that the curves graphed here are for illustrative purposes only - the equations for musketry and riflery are so simple that their usage becomes second nature after only one or two tries. There is no need to look up any data on the graphs themselves. There are gamers who might shudder at use of the term "equation" and its implication of a complex mathematical formula, but here, for example, in the "equation" (ughl) for rifle fire, 30 - range, what could be simpler than merely subtracting the measured range from 30 to determine P(r)?? THE EFFECT OF COVER The musket and rifle fire equations discussed thus far are for lean and Pierre potting away at targets in the open. If the target is behind hard cover-protected by walls or within a house-I use a negative modifier, -8, to reduce the probability. Thus P(m) for musketry becomes: P(m) = 2 (15 - range) - 8 Another way of writing this results from "absorbing" the B into the parenthesis: P(m) = 2 (11- range) The graph of this equation is compared with the original in Figure 4. 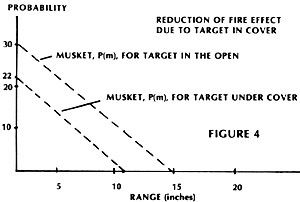Examination of Figure 4 yields some interesting results: a. The maximum range for a target under cover has fallen off from 15 inches to 11 inches, i.e., 150 yards to 110 yards. b.The maximum probability at point blank range has fallen off from 30% to 22%. This does not mean that Jean and Pierre's muskets, in some mysterious fashion, no longer reach out to 150 yards. It does mean, however, that for all practical purposes, the P(m) beyond 110 yards is zero for a man crouching behind a wall because of the combined effect of reduced target size and increased protection. Similarly, the drop in accuracy results from this same target obscuration. ARTILLERY, CANNISTER The fire effect of cannister, P(C), is modeled by using the same equation as for rifle fire: P(C) = 30 - range Cannister thus reaches out, like riflery, to 300 yards. Here, too, the maximum probability, at point blank range, is 30%. The question immediately arises: how, with a maximum P(C) of 30%, do we model the horrendous effects that short range cannister should have on targeted troops? The answer comes about from a consideration of the relative firepower effects involved. The cannon casting and its crew of figures represents a battery of guns; its effect, therefore, must be multiplied to obtain the same result that would have occurred had the entire battery blasted away. To a first order approximation, the casualty rate inflicted by an entire battery firing cannister may be equated to that inflicted by a unit the size of a battalion. What I do, therefore, is to: a. DMan each gun with 6 artillerist castings. b. Decree that each fire effect of the gun is obtained by multiplying the number of artillerymen castings by a factor of 3. In essence, therefore, each gun becomes a concentrated source of firepower stemming from 6 x 3, or 18 figures. An unfortunate target unit at, say, 10 inches, would suffer considerably: P(C) = 30 - range = 20% per man POH = 18 effectives x 20% = 360% Thus the loss would be 3 sure hits plus 60% chance of a fourth. This is an appreciable diminution of a 20 man unit, especially in light of the fact that the gun would get to fire at least twice as the target unit advances within the 30 inch cannister range. Any reasonable set of morale rules would produce an extremely low probability of the target unit closing with the battery after having been bumped several times in such fashion. The moral, one that Lord Cardigan learned the hard way . . . "Don't charge the guns!" Of course, as the battery itself takes casualties, its firepower effect decreases . . . every casting killed reduces the multiplier, i.e., the number of effectives, by 3, which simulates the individual guns of the battery gradually being silenced. ARTILLERY, ROUNDSHOT One last item remains . . . the treatment of roundshot, P(R). Here, two considerations apply: a. First, the P(R) curve must be such that the fire effect of roundshot, closein, is less than that of cannister. b. Second, the range of effective roundshot need be no more than 600 to 800 yards . . . not because the guns couldn't reach further, but because the inherent inaccuracies of the weapon, coupled with the haze of battle, made firing at longer ranges ineffective. 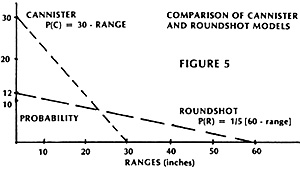The equation chosen to represent the fire effect of roundshot, P(R), takes the same form as those previously discussed but permits a much longer range, as indicated in Figure 5: P(R) = (1/5) (60 - range) Note that the P(R) curve has the following attributes: a. The maximum range extends out to 60 inches, or 600 yards. b. The maximum P(R), at "zero" range, is 12%. c. The P(C) curve crosses the P(R) curve at 22.5 inches. Item (c) is most important, for, at ranges less than 22.5 inches, or 225 yards, P(C) is greater than P(R) and the battery commander should fire cannister to benefit from the larger P(C) value. Conversely, the c~annister effect dies out rapidly at ranges greater than the 225 yard crossover . . . hence at these ranges, roundshot is the required load. As item (b) indicates, the P(R) curve values are purposely kept low to prevent the artillery from "taking over the game". The values are not so low, however, as to make the battery completely ineffective. For example, at 50 inches, or 500 yards: P(R) = (1/5) (60 - 50) = (1/5) (10) = 2 percentage points per man. And for the artillery crew of 6, each one of which acts as 3 men: POH = 18 effectives x 2% = 36%. A 36% chance of losing a figure, while not overwhelming, is certainly not to be ignored. If a battery was so unfortunate as to use up all its cannister and was forced to fire roundshot at an oncoming target the fire effect, at point blank range, would be: P(R) = (1/5) (60 - 0) = 12 percentage points per man POH = 18 effectives x 12% = 216% On the average, therefore, this final blast would result in 2 hits. Compare this to the point blank cannister effect: P(C) = 30 - 0 = 30 percentage points per man POH = 18 effectives x 30% = 450% FINAL THOUGHTS The methods presented in this article are exceptionally easy to implement during a battle. Additionally, the techniques are quite adaptable to other scales, other systems. For example, would you like to extend the roundshot effect out to 800 yards? Very well, then P(R) = (1/5) (60 - range) becomes P(R) = (1/5) (80 - range). Or perhaps, you feel that cannister should reach out to 400 yards. Then P(C) = 30- range becomes P(C) = 40 - range. With the advent of percentage dice, we're not restricted to the 16% increments resulting from adding and subtracting "ones" and "twos" to a six-sided die. Hence there is no logic for sticking to the staircase fire effect curve depicted in Figure 1. The real world uses smooth curves, and so should the model on the wargaming table. Indeed, the linear curves discussed are simplistic in scope, and more accurate results would be obtained by using higher order equations. But for a first cut, straight line techniques provide enough complexity until the concept becomes familiar to a sufficient number of gamers. The author would appreciate hearing from those who have tried, and can comment on, the thoughts presented here. Back to Table of Contents -- Courier Vol. 2 #6 To Courier List of Issues To MagWeb Master Magazine List © Copyright 1981 by The Courier Publishing Company. This article appears in MagWeb (Magazine Web) on the Internet World Wide Web. Other military history articles and gaming articles are available at http://www.magweb.com