 Probably one of the most agonizing moments in armor
miniature games comes when a hit has been scored and
the time comes to compare the penetration capability of the
shell with the armor it struck. It is at this juncture of the
game that, much to bewilderment of many players, life or
death for the poor tanks and armored cars becomes quite
literally a matter of millimeters (1/25th of an inch).
Probably one of the most agonizing moments in armor
miniature games comes when a hit has been scored and
the time comes to compare the penetration capability of the
shell with the armor it struck. It is at this juncture of the
game that, much to bewilderment of many players, life or
death for the poor tanks and armored cars becomes quite
literally a matter of millimeters (1/25th of an inch).
As an example, you're playing a game with TANK CHARTS (or just about any other rule system that compares shell AP to armor thickness). A PzKw IIId has just landed a 37mm round on the front upper hull of a Somua, at 275 meters range. According to the armor mechanics of the ruleset, the 500 meter range penetration figure for the 37mm L/45 gun is used as the guns' "punching power" (a real lightweight, by the way), which cross references to 39mm of armor penetration. Since the Somua has 40mm of hull armor at the point where the shot landed, no damage has been caused due to the effect of one silly little millimeter of armor.
In just about all rule systems of this type, the effectiveness of guns is reciuced to a "hit or miss" affair based on whether the precise amount of armor carried by the target can be equaled. This is not only somewhat illogical due to a number of other factors that have been left out of the analysis (angle of impact, use of 500 meter range although hit at 275 meters, etc.), but also implies that penetration data can be figured out with the precision of a moonshot, which it obviously can't. Each round will probably differ by a tiny bit in penetration, and in the Somua- PzKw IIId case, an increase of 2.5% in penetration would have succeeded.
Having suffered through a multitude of "hair-splitting" victories or defeats that hung on one millimeter of armor in our France, '40 games, our group decided to work out a procedure that would take account of many of the factors that play an important role in determining whether a shell penetrates.
| TABLE I -- GENERAL AP EFFECTS | |
|---|---|
| Shell Penetration AP Ratio armor thickness | Maximum Die Roll Score for "Kill" (2d6 dice) |
| 0.0-0.8 | 2 |
| 0.8-0.9 | 3 |
| 0.9 - .95 | 4 |
| .95 - 1.05 | 7 |
| 1.05- 1.10 | 7 |
| 1.10-1.20 | 8 |
| 1.20-1.30 | 9 |
| 1.30-1.50 | 10 |
| 1.50 + | 11 |
| Shot Size and Characteristics Under41mm; add "+1" to roll Non-explosive; add "+1" to roll | |
| Immobilization Effect Rolling the highest kill score results in an immobilization of thetarget vehicle | |
Take the case where the 500 meter penetration figure
is exactly equal to the armor it hit. If the range is between
250 and 500 meters, the shell penetration can range from
10-15% higher depending upon where in the range interval
the shot was made. A 250 meter range increment is used
for playability, since a million arguments would ensue if
tape measurements came down to the nearest 1/4 inch.
There is also a small chance that the round will have a little
more speed so one might except a +10-20% greater
penetration. [1]
Negative Side
For our analysis we utilized the results from a 1948
U.S. Army Technical Manual (TM-1917) that provided highly
detailed accounts of proving ground tests of shell
penetration. An analysis of the effect of angle on
penetration indicated that 30 degree obliquities (a really
fancy word) increased armor resistance by about 25%,
more than what the traditional 1/COSINE forumla would
predict (about 12%). [2]
This infers that not only does armor
effective thickness increase rather rapidly with angle as one
deviates from the target facing, but angle effects can
overcome the effects of reduced range within an interval as
the angle of incidence of the hit increases (a 20 degree
angle increases armor by roughly 15%).
In view of the proceeding, it was decided to use a
method somewhat similar to the CROSS OF IRON
approach (kill probabilities represented by dice roll scores),
but heavily dependent on an analysis of shell penetration
versus armor, damage tendencies of rounds, and the
factors that were identified above.
After much experimentation, Table I was prepared as
the basis for our system:
To explain the charts' subtleties, the AP Ratio signifies
the ability of a given round to overcome the effects of angle
on armor thickness and still equal or exceed the value
needed for a penetration.
As the ratio goes up, the shells should penetrate
greater percentages of the time, leading up to a 97%
chance by rounds that "overpenetrate" more than 50%
(damage is dependent on the "overkill," to a degree, since a
round with a lot of power left after entering a tank will
probably do more in the way of significant damage than a
shell that just made it through and fragmented on the way).
The ratios less than 1 introduce an idea that is fairly
interesting, since rounds that theoretically should fail to
penetrate have the ability to do some major damage. In the
case of ratios from 0.0 to .95, the main effect of hits will be
to immobilize the target, which is probably a track hit that
separates the treads from the wheels (even a 20mm round
has a chance of detracking a Tiger II, although here it is
less than 3%).
From .95 to 1.05, we're dealing with shells that
theoretically are right around the value needed to penetrate,
and the real difference between them is small (.95 of 40mm
is 38mm, the case where the shell failed to penetrate by
2mm in a strict comparison). This range takes into account
the often "hairy" case where one fails or succeeds based
on a millimeter by millimeter analysis, and it introduces
some "reasonableness" into the results.
Although these ratios are straddling the number needed
to pierce the basic armor thickness, any angle at all on the
hit will likely deflect the hit, and they are going to penetrate
(if they do) with a low lethality, so the "kill" probability is
only 28% (roll 5 or less with two die).
In addition, of the 28% of rounds that do some
worthwhile damage, about half will only immobilize the
target, which corresponds to the case where hits get into
the turret or hull with a minimum of kinetic energy left to
generate useful mayhem.
Special Modifiers
Owing to the mass of the rounds, one would expect the
heavier and larger shells to do more damage after getting
into a tank owing to more bits of metal blowing about, and
more explosive power when they explode (many AP rounds
had primers and HE charges for added killing power). While it could penetrate quite a bit of
armor, the 2 pounder round was solid, which decreases its
effect somewhat due to the lack of a follow-up explosion
inside the penetrated tank. Thus, its lethality suffers
penalties with regard to shell size and explosive power,
allowing some penetrated targets to roll along unperturbed
after being hit by 2pdr rounds.
Having prepared a basic system that relates shell
penetration and size effects with damage potential, one
then has to apply it to target armor in order to prepare
scores that can be used in games. The problem of
developing vehicle specific kill scores was then solved by
copying down the armor and weapon penetration data from
a popular set of armor miniature rules (TANK CHARTS),
and comparing the AP Ratios to the die scores previously
decided upon.
Example
As an example of the process, the French 47mm gun
could blast through 45mm of armor at 500 meters (an
average range in our games), and a common target was the
German PzKw IIId (which had 32mm frontal armor). With
45mm of penetration and a 32mm thick target, the AP Ratio
is 1.41, which corresponds to a kill score of 10 (83%
chance of a "kill," 9% for an immobilization). This procedure
was then carried out for every gun and major armor plate for
the vehicles that fought in 1940 France, and the following chart was prepared:
NOTES
Illustration
To illustrate the use of the procedure, say a Somua has
hit a PzKw IVd in the front at a range of 650 meters. From
the chart, the unmodified kill score is a 10, which then is
reduced by one due to the range and the shell size. Thus,
rolling 2-8 (72%) will destroy the unlucky panzer and a roll
of 9 (11 % chance) will stop the German tank in its tracks.
Although this method pretty much incorporates the
share of hits that will land on the tracks, the turret/hull split
has yet to be determined. For simplicity, assume that one-third of the frontal hits will bounce up against the turret,
and one-sixth of the flank hits (treat the rear like the front).
Therefore roll one colored die with the regular die To Hit roll,
with scores of 1 or 2 on frontal/ rear hits and 1 on flank hits
indicating a turret hit (if hulldown, increase the range of rolls
needed for a turret hit by three (1-5 for frontal, 1-4 for flank).
Range Modifications
A few words about the range modifications are in order
since some results might be hard to rationalize. For
instance, 700 meters was chosen as the limit beyond
which a single modifier is used since very few hits (except
by 88's) that mean anything will be made much beyond that
range (37mm guns are fairly worthless much after 800 meters), and 88's don't decrease in killing power all that much.
To show how this method stacks up against a mathematical comparison of AP versus armor (where AP must equal or exceed armor for damage), the following chart was put together. The results were taken from TANK CHARTS:
Most of the differences in damage effects are due, in
part, to the fact that 37mm rounds are highly penalized
under our approach, while the armor miniatures ruleset
treats 20mm rounds exactly the same as it does 47mm. In
addition, most armor rules treat a through penetration of
armor exactly the same as a partial penetration, while
we've differentiated between clean penetrations (where the
round easily pierced the plate due to an abundance of
"zing") and minimal breakthroughs (where the round hardly
manages to get inside the vehicle).
While there are a number of factors that would seem to
indicate that our approach is superior to other rules, it
should be noted that so much of this material is subjective
and based on personal guesses, and that it is impossible
to say "this is right, and that is wrong."
TANK CHARTS, despite widely disparate results, is
just as "correct" insofar as it is consistent with the
designers' view of what is important and is likely to occur,
which just points out the tremendous subjectivity of rule
design. Owing to our interest in allowing rounds to cause
damage even if their penetration is 1 or 2 millimeters
short, we've chosen to take a different approach which
must of necessity create different results.
The Char B1 had an engine grill on the left flank of the
vehicle that formed a sort of "Achilles Heel," and enabled
the German 37mm anti-tank guns to disable the tank. This
weak spot can be modeled by increasing the flank Kill
Score by "2" whenever a hit is made on the left side armor
(the left as one is sitting on the rear of the AFV facing the front).
In addition, the 75mm gun carried by this tank only
fired high explosive rounds (HE), which could severely
damage the lightly armored vehicles it was up against. The
lethality of the 75mm HE can be incorporated by treating its
kill score as a "6" against all target vehicles (the problem is
mostly in hitting targets, since the 75mm gun was "fixed,"
in the literal sense, and useless against moving targets).
Treating rolls of 5 and 6 as immobilizations.
As a bit of general clarification, immobilization of a
tanks' turret (as opposed to hull immobilization, which
wipes out the movement capability) not only eliminates the
target's turret weapons, but may wipe out the turret crew
(roll one die, with 1-3 killing the turret crew and leading to a
bailout of the rest of the crew). Hull immobilizations stand a
fair chance of causing a crew bailout, so roll the one die
and 1-2 scatters the entire crew.
by Rod Burr
[1] 1. A variation of + or - 10-
15% is plausible due to munitions quality and other factors.
Note: Round weight is a function of the diameter cubed (diameter
x diameter x diameter) for shells of the same shape when comparing
guns of significantly different lengths in calibers, a conversion factor
of the ratio of the calibers should be included.
 On the negative side, most frontal shot definitions allow
frontal hits to land at thirty degree angles to the target
facing, which increases the effective armor thickness by 12-
25% (depending upon whose data one uses) due to the
ballistic effects of angled hits on effective armor thickness
for penetration. Once again, shell variations from the
average case are just as likely as to be decreases as
increases, which can cancel out some of the bonus we
previously considered.
On the negative side, most frontal shot definitions allow
frontal hits to land at thirty degree angles to the target
facing, which increases the effective armor thickness by 12-
25% (depending upon whose data one uses) due to the
ballistic effects of angled hits on effective armor thickness
for penetration. Once again, shell variations from the
average case are just as likely as to be decreases as
increases, which can cancel out some of the bonus we
previously considered.
 The special modifiers at the bottom of the chart are
there to introduce certain shell characteristics into the
results, based on shell size and internal make-up. For
instance, rounds up to 40mm in diameter generally weighed
about 1.0 to 1.5 pounds, compared to the 4-5 pound range
exhabited by 47-57mm shells (the 88mm shell is quite a bit
larger. [3]
The special modifiers at the bottom of the chart are
there to introduce certain shell characteristics into the
results, based on shell size and internal make-up. For
instance, rounds up to 40mm in diameter generally weighed
about 1.0 to 1.5 pounds, compared to the 4-5 pound range
exhabited by 47-57mm shells (the 88mm shell is quite a bit
larger. [3]
TABLE II -- FRANCE '40 AP EFFECTS
FRENCH AND BRITISH WEAPONSTarget 47mm 37mmL/33 37mmL/21 2 pounder PzKw 38t 11/11 9/9 4/4 9/9 PzKw 35t 11/11 9/10 4/10 9/9 PzKw IIId 10/10 7/7 3/3 9/9 PzKw IVd 10/11 7/10 2/48 9/9 PzKw IIb 10/11 7/10 2/10 9/9 Small Targets 11/11 10/10 10/10 9/9
TABLE II -- FRANCE '40 AP EFFECTS
GERMAN WEAPONStarget 47mmL/43 37mmL/45 75mmL/24 88mm
20mmL/55 Somua 4 10/5-10 2-4/2-4 5-10/9-10 11/11 2/2 H35 8-10/5-10 3-7/3-6 9-11/8-11 11/11 2/2 H39 7-10/5-10 3-7/3-6 8-11/8-11 11/11 2/2 Char B1 bis 42/5-3 2/2 5-3/8-3 11/11 2/2 Matilda I 3/3 2/2 4-5/4-5 11/11 2/2 Matilda II 2/2 2/2 2/2 11/11 2/2 A10 11/11 9/9 11/11 11/11 2/2 Small Targets 11/11 10/10 11/11 11/11 10/10 1: Small Targets include MG Tanks, halfbacks, armored cars, and other vehicles with less than 20mm of armor
2: Number to left of slash is frontal armor, to the right is the flank and
rear armor plate (roughly equivalent for our purposes)
3: Where two numbers are on one side of the slash, the first is the kill score against the turret, the second against the hull.
RANGE MODIFIERS Range Shell Diameter Add to Kill Roll 0-240m any -2 501-700m under 41 mm +2 501-700m over 41 mm +1 701m and beyond under 41 mm +3 701m and beyond over 41 mm +2  The -2 add-on within 240 meters will jack up kill numbers high enough so that PzKw II's will have a 17% chance of damaging Matilda's a seemingly illogical result if armor penetration is considered. Within 240 meters the chance of hitting tracks usually goes up as a generai rule
(the effect of furls in the ground towards screening the lower reaches of a tank are minimized), and given the rate-of-fire of the mini-tanks of 1940, a track "kill" is a good possibility (half the kills with a score of "4" will be track tears). Armor penetration for small guns also goes up tremendously within 240 meters as compared to the 500 meter value used
in the analysis, so a good-sized bonus is needed to "accurately" portray the increase in killing power at short range.
The -2 add-on within 240 meters will jack up kill numbers high enough so that PzKw II's will have a 17% chance of damaging Matilda's a seemingly illogical result if armor penetration is considered. Within 240 meters the chance of hitting tracks usually goes up as a generai rule
(the effect of furls in the ground towards screening the lower reaches of a tank are minimized), and given the rate-of-fire of the mini-tanks of 1940, a track "kill" is a good possibility (half the kills with a score of "4" will be track tears). Armor penetration for small guns also goes up tremendously within 240 meters as compared to the 500 meter value used
in the analysis, so a good-sized bonus is needed to "accurately" portray the increase in killing power at short range.
Range 37mmL/45
PenetrationSomua Front
Hull Armor%KO %Immobilize 0m. 54mm 40mm 33%(28%) 50%(15%) 230m 43mm 40mm 33%(28%) 50%(15%) 500m. 39mm 40mm 0% (9%) 0% (8%) 600m. 36mm 40mm 0% (3%) 0% (5%) To compare, the percentages given by our method are in parenthesis. 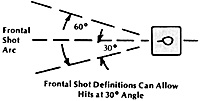 Players wishing to use the AFV Kill Scores
provided in this article can add them to their usual
games (although it's somewhat unusual to play 1940
scenarios given the appeal of Barbarossa and Normandy),
using the hit process their normal rules provide but
substituting the Kill Scores for the AP/armor comparisons.
If nothing else, these rules add some unusual
considerations into the damage determinations used in our
armor gaming, and gives the nitpicker types something to
study and improve upon.
Players wishing to use the AFV Kill Scores
provided in this article can add them to their usual
games (although it's somewhat unusual to play 1940
scenarios given the appeal of Barbarossa and Normandy),
using the hit process their normal rules provide but
substituting the Kill Scores for the AP/armor comparisons.
If nothing else, these rules add some unusual
considerations into the damage determinations used in our
armor gaming, and gives the nitpicker types something to
study and improve upon.
TABLE IIl -- FRANCE '40 DATA Gun 500 meter
PenetrationTank Front Armor Side Armor Turret Hull Turret Hull 20L/55 25mm PzKw IIb 30mm 31mm 17mm
15mm 37L/45 39mm
(tank gun)
German 42mm
AT gun &
38t weapon
'Czech*'PzKw IId 32mm 32mm 36mm 30mm PzKw 35t 26mm 27mm 16mm 16mm PzKw38t 25mm 25mm 25mm 25mm PzKw IVd 32mm 32mm 24mm 20mm PzJg I 15mm 15mm 15mm 15mm H35 45mm 35mm 50mm 37mm 37L/33 36mm H39 49mm 35mm 50mm
37mm 75L/24 57mm Somua S35 56mm 40mm 51mm 39mm 47L/P43 52mm Char B1 bis 56mm 66mm 51mm
60mm 37L/21 23mm - 47L/34 45mm - * The higher penetration for the Czech gun is
due to the solid AP rounds heavier weight due to the absence of any
expensive charge. Source: TANK CHARTS armor ruleset. CHAR B1 BIS Special Notes
EDITOR'S NOTES
[2] 2. To a large degree this
reflects glancing/deflection, as well as the geometric effects
represented by 1/cosine.
[3] 3. I would use under 70mm
rather than 41mm. There is a much more dramatic change here than
between 37mm and 50mm. The bursting charges for German APHE
rounds are:
Charge Weight 37mm 13 gm 6830 gm 50mm/L42 16.4 gm 20600
gm 75mm/L48 82 gm 68000 gm
Back to Table of Contents -- Courier Vol. 2 #3
To Courier List of Issues
To MagWeb Master Magazine List
© Copyright 1980 by The Courier Publishing Company.
This article appears in MagWeb (Magazine Web) on the Internet World Wide Web.
Other military history articles and gaming articles are available at http://www.magweb.com