Armor penetration, especially for tank battles, has been a perpetual problem among wargamers and wargame designers. For some reason, ballistics is not a standard high school or college topic, and many wargamers thus deprived of the mathematical background needed. This forces one to rely on the driblets of data that has appeared in print, or on personal guesses derived from all sorts of speculative sources, sometimes laced by a general comparative feel for the weapons involved.
Now it is possible to compute armor penetration from the gun size, muzzle velocity, and shell weight alone. If you have actual penetration data for one or two ranges, this can be used to find precise characteristics for the gun, and produce equally accurate penetration data for any range.
Surprisingly, the ballistic calculations aren't too complex. This is because tank duels normally involve high-velocity guns at short ranges punching through simple homogeneous armor plate, resulting in flat trajectories for the shells (a great simplification), and hopefully not too much variation on the part of the armor.
Only one equation need be used to compute armor penetration:
where: w=weight of the shell (in pounds); d=diameter of gun (in inches); K = special constant derived from tables with this article.
The tables used to find K are based on muzzle velocity of the gun (in feet per second) and range at which the target is hit, so muzzle velocity must be known as well as the shell weight and gun size.
| K Values Chart | |||||||
|---|---|---|---|---|---|---|---|
| muzzle velocity feet/sec | range at which penetration is being calculated (in yards) | ||||||
| 0 | 500 | 1,000 | 1,500 | 2,000 | 2,500 | 3,000 | |
| 500 | 6.75 | 6.07 | 5.46 | 4.91 | 4.41 | 3.96 | 3.55 |
| 600 | 8.88 | 7.98 | 7.19 | 6.46 | 5.80 | 5.21 | 4.67 |
| 700 | 11.21 | 10.08 | 9.07 | 8.15 | 7.32 | 6.57 | 5.90 |
| 800 | 13.71 | 12.33 | 11.09 | 9.97 | 8.96 | 8.04 | 7.21 |
| 900 | 16.37 | 14.57 | 13.08 | 11.77 | 10.59 | 9.53 | 8.57 |
| 1,000 | 19.19 | 16.85 | 14.97 | 13.42 | 12.07 | 10.86 | 9.77 |
| 1,100 | 22.16 | 18.85 | 16.59 | 14.76 | 13.23 | 11.90 | 10.71 |
| 1,200 | 25.27 | 20.66 | 17.90 | 15.83 | 14.12 | 12.69 | 11.42 |
| 1,300 | 28.51 | 22.40 | 19.00 | 16.70 | 14.85 | 13.31 | 11.98 |
| 1,400 | 31.88 | 24.32 | 20.13 | 17.52 | 15.50 | 13.87 | 12.46 |
| 1,500 | 35.38 | 26.46 | 21.32 | 18.29 | 16.18 | 14.41 | 12.94 |
| 1,600 | 39.00 | 28.99 | 22.68 | 19.17 | 16.82 | 14.95 | 13.40 |
| 1,700 | 42.73 | 31.70 | 24.20 | 20.05 | 17.48 | 15.49 | 13.84 |
| 1,800 | 46.58 | 34.54 | 25.97 | 21.02 | 18.13 | 16.02 | 14.28 |
| 1,900 | 50.53 | 37.53 | 27.98 | 22.15 | 18.82 | 16.57 | 14.73 |
| 2,000 | 54.60 | 40.65 | 30.17 | 23.32 | 19.54 | 17.11 | 15.18 |
| 2,100 | 58.77 | 43.86 | 32.57 | 24.71 | 20.33 | 17.66 | 15.64 |
| 2,200 | 63.04 | 47.23 | 3s.06 | 26.31 | 21.20 | 18.26 | 16.10 |
| 2,300 | 67.41 | 50.69 | 37.68 | 28.03 | 22.16 | 18.85 | 16.59 |
| 2,400 | 11.88 | 54.27 | 40.37 | 30.00 | 23.21 | 19.48 | 17.07 |
| 2,500 | 76.44 | 57.91 | 43.18 | 32.05 | 24.42 | 20.18 | 17.57 |
| 2,600 | 81.10 | 61.68 | 46.15 | 34.21 | 25.75 | 20.92 | 18.08 |
| 2,700 | 85.85 | 65.47 | 49.17 | 36.50 | 27.27 | 21.73 | 18.59 |
| 2,800 | 90.69 | 69.41 | 52.23 | 38.87 | 28.91 | 22.63 | 19.14 |
| 2,900 | 95.62 | 73.44 | 55.49 | 41.35 | 30.69 | 23.61 | 19.72 |
| 3,000 | 100.63 | 77.58 | 58.77 | 43.92 | 32.60 | 24.75 | 20.36 |
| 3,100 | 105.73 | 81.83 | 62.22 | 46.61 | 34.60 | 25.95 | 21.05 |
| 3,200 | 110.92 | 86.17 | 65.73 | 49.37 | 36.67 | 27.37 | 21.77 |
| 3,300 | 116.19 | 90.58 | 69.33 | 52.20 | 38.82 | 28.88 | 22.60 |
| 3,400 | 121.54 | 95.06 | 72.99 | 55.13 | 41.07 | 30.49 | 23.49 |
| 3,500 | 126.97 | 99.67 | 76.84 | 58.21 | 43.44 | 32.19 | 24.49 |
| 3,600 | 132.48 | 104.30 | 80.63 | 61.28 | 45.84 | 34.01 | 25.63 |
Having the numbers in the proper size units is of vital importance for these equations, since exponents are involved. Most gun sizes are given in millimeters (mm's) and this must be divided by 25.4 to convert to inches. Similarly, shell weight must be in pounds, so that ounces must be converted to fractions of a pound (thus 1 lb. 8 oz. would become 1.5 Ibs.), or kilograms (kg) multiplied by 2.2046 to get pounds. Muzzle velocity must be in feet per second (fps), if in meters per second (mps) multiply by 3.2808 to get fps.
With everything in the proper units, begin the equation itself. The hard part is calculating that first exponential subtotal. Start with the gun's diameter (d) and cube it (i.e., "d" times "d" times "d"). Then divide this into the weight of the shell. The overall total must then be raised to the 0.75407 power. The easiest way is to beg, borrow, or buy a "slide rule" electronic calculator capable of variable exponents (one with a "yx" or "xy" key). Lacking this, you'll have to use logarithm tables. Find the logarithm for your total (w/d3) and multiply it by 0.75407. The result is another logarithm, and you must go back to the tables and convert it into a "real" number again for your result.
This subtotal is then multiplied by the diameter of the gun (d), and then multiplied again by the K value. The final total is the millimeters of armor the gun can penetrate, assuming the shell hits the armor straight on.
Using the K value chart is very simple: crossreference the muzzle velocity of the gun with the range to get K. For ranges or muzzle velocities other than those given on the table, interpolation is necessary. This means computing the difference between K's, for example, and taking a proportion of that equivalent to the proportion of difference between the range you want and the table. Take the K differences as a proportion of the difference between muzzle velocities if that is the variable, or do it as a two-step process if both muzzle velocity and range fall between the values given on the table.
EXAMPLE: the WWI I German 50mm/L60 PaK 38 or KwK 39 tank and anti-tank gun has a 4.96 lb shell and a muzzle velocity of 2700 fps. The 50mm gun, converted to inches, is 1.97.
Start with d3; so 1.97 x 1.97 x 1.97 ù 7.645. Next, find w/d3, or 4.96/7.645 ~ 0.649. This raised to the 0.75407 power is 0.722. Multiplied again by d = 1.97 it becomes 0.722 x 1.97 = 1.422. Now go to the table, using the 2,700 fps line. At 500 yards, K = 65.47, so penetration is 1.422 x 65.47 = 93mm. At 1,000 yards penetration is 1.422 x 49.17 = 70mm. Note that only K varies with range, making computation of penetration at various ranges for the same gun relatively easy.
To find penetration at 800 yards, interpolation is needed. 800 falls between 500 and 1000, so that its proportion of the difference in the ranges is (800500)/1000-500) = 300/500 = 0.6. The difference between K's at 500 and 1000 yards is 49.17-65.47 = - 16.30. The proper proportion of the K difference is therefore -16.30 x 0.6 = -9.78. Therefore K at 800 yards is 65.47-9.78 = 55.69. This produces a penetration value of 1.422 x 55.69 = 79mm.
ANGLE OF FIRE & ARMOR SLOPE
The basic armor penetration above gives the maximum possible for the gun. However, rarely is a gun directly facing an armored target, but instead it is usually a few degrees off to the left or right. This not only increases the chance the shell might bounce off, but also means the shell has to cut through the armor at an angle, being forced to penetrate more armor.
Superficially, this would seem to be a simple trigonometric calculation where penetration is dividied by the cosine of the angle (where 0 degrees means shooting straight on, and 90 degrees shooting parallel to the armor, and thus unable to hit; if 90 degrees is taken to mean shooting straight on, divide by the sine instead of the cosine of the angle).
Alas, peculiar things happen when a shell hits armor. As it crunches through, its path actually bends, along the line of least resistance, in effect "straightening out" along a better line, reducing the influence of the angle and the effective armor to be penetrated. Furthermore, against homogeneous plate, once the first crack is made (i.e., any penetration) a splitting effect occurs. This can be reduced to a function of penetration also (due to the homogeneous armor) and results in a somewhat better overall effective penetration.
The influence an angle has, first calculated trigonometrically, and then with the "straightening" effects, is given in figure 1.
Figure 1: Effect of Slope/Angle on Penetration
| Angle | trigonometric penetration percentage | straightened penetration percentage |
|---|---|---|
| 0 degrees | 100% | 100% |
| 5 degrees | 99% | 100% |
| 10 degrees | 98% | 99% |
| 15 degrees | 97% | 98% |
| 20 degrees | 94% | 96% |
| 25 degrees | 91% | 94% |
| 30 degrees | 87% | 92% |
| 35 degrees | 82% | 89% |
| 40 degrees | 77% | 85% |
| 45 degrees | 71% | 81% |
| 50 degrees | 64% | 76% |
| 55 degrees | 57% | 72% |
| 60 degrees | 50% | 67% |
This same system can be used to calculate the effect armor slope has on penetration, where 0 degrees slope means vertical (unsloped) armor (i.e., the degree measure is the amount of slope compared to the vertical). Normally both slope and firing angle combine, so that the percentage of penetration from each should be multiplied together. For example, using trigonometric penetration values of figure 1, if the gun fires at 20 degree angle (94%) at armor with a 45 degree slope (71%), the result is .94 x .71 = 66.7% penetration. However, for simplicity most wargamers prefer to compute the effect of armor slope right into the armor value, for the "armor basis" (thickness times the effect of slope, which is the inverse of the percentages given). For example, using trigonometric percentages again a German "Panther" tank with 80mm frontal hull armor, at a 55 degree slope has an armor basis of (80)x(1/0.57) = 140mm. Then, on the average, tank guns can be assumed to be firing from 15-30 degree angle, and their normal penetration reduced by that amount.
Actually, all these calculations are semi-futile because many additional factors influence armor penetration. This is because when the path of the shell bends, so does its effective velocity change, which decreases penetration. Further, the shot breaks up on its way through, reducing its force logarithmically, and in ways peculiar to each type of shot. Tests of German guns indicate that at a 30 degree angle, penetration is really only BO% normal, less than either the trigonometric or straightened value. Because angular penetration is peculiar to each gun and shell type, penetration data does sometimes give some angular measure, so you can find the proper percentage, and then relate that to the trigonon~etric or straightened value to give proper percentages for any angle.
ON KILLING TANKS
Tank armor data normally gives armor plates covering the main areas: front, side, and rear of the hull and turret (or superstructure on turretless vehicles), sometimes further categorized into upper and lower hull (that covered or uncovered by the tracks and wheels) etc. However, in any tank there are numerous small chinks and weak points, including vision slots, gun mantles edges, periscopes, turret ring, and even the gun barrel itself.
It is very tiresome on the wargame table to use "special hits" dice to account for all such chinks, and the general preference is to increase penetration somewhat to account for it, on the assumption that the chinks are proportionately weaker than the main armor, and/or to permit killing hits beyond basic penetration range, but at a vastly reduced probability. The former will allow you, for example, to justify using trigonometric values when computing firing angle or armor slope angle percentages, thus simplifying that task considerably, if at the expense of some strict accuracy.
Early in WWII, and before, some tank armor was riveted together, and when hit by shells, the rivets sometimes popped, causing all sorts of unfortunate results. By 1942 even the Russians had largely abandoned that form of armor in favor of welded plates of rolled steel, if not one-piece steel castings.
Also bear in mind that tank tracks and running wheels are extremely easy to damage, as it takes little to pop a track pin, or bend a wheel enough to chew up the track and break it. Only in rare cases will a crew attempt to fight from an immobilized tank, so regardless of penetration ability, almost any gun has a chance at immobilizing a tank if its running gear is exposed.
Finally, the top deck and turret roof armor of tanks is generally very thin (1~15mm) and becomes a vulnerable point to fire from superior elevations and/or aircraft attacks. The engine grates to the rear of the vehicle are an especially vulnerable point.
SPECIAL AMMUNITION
This penetration information is based on "standard" WWII armor piercing ammunition, which were armor-capped rounds with some explosive power. This was different from "HE" high explosive rounds, which had only a thin cap and a contact exploder, often with shell walls designed to disintegrate on explosion into shrapnel-size fragments for maximum anti-personnel effect. Such ammunition always exploded against armor, but a big shell against weak armor, by the very force of the blast, might bend the armor enough to break it open. Even if it didn't, the concussion effect on the crew was often quite impressive, and hits on the running gear by a shell of significant size (70mm or larger) were normally disabling.
Late in the war, the Americans, British and Germans began using special ballistic caps on their ammunition. This improved the flight characteristic of the ammunition, which increased terminal velocity (speed at which the shell hit the target), and thus the penetration. If you can find any penetration data for guns using such ammunition, the ballistic coefficient (C) can be calculated and applied to all armor penetration, as described in the next section. Almost all modern armor piercing ammunition incorporates some sort of special ballistic cap.
The final improvement on basic AP (armor piercing) rounds was the "discarding sabot" concept. The idea here is that the shell has a narrow core inside the wider normal-sized shell jacket, which flakes off as the round leaves the muzzle. Thus the force of firing the round is transferred to the narrower "bolt", which gets that much more penetrating power because the force is concentrated in a smaller area. The Germans used tapered bore guns, such as the sPzB 41, into whose 28mm wide breech fitted a 28mm wide shell, but only a 20mm wide bolt emerged from the muzzle (also only 20mm wide), so that the compression in the barrel caused the excess diameter to flake away and spit out the muzzle as excess flash. Unfortunately, this gun as well as the traditional discarding sabot rounds (AP40 type) used in normal guns, consumed great quantities of tungsten, which the Germans did not have, and thus had virtually disappeared from service after 1942.
It wasn't until 1944-5 that the British followed by the Americans began introducing APDS (discarding shot) rounds for their guns, normally in an attempt to upgrade poorer quality weapons. Most modern tank guns carry APDS as a matter of course, and it is usually the prime anti-tank round.
Mathematically, the original (before-firing) shell diameter should be used for APDS rounds. Although these shells are lighter than normal ones, they get a much higher muzzle velocity, which more than compensates. Unfortunately, the K values cannot be adjusted for the smaller "bolt" without extremely difficult mathematics, but at least you can represent the better penetrating power of the smaller bolt by using "straightened" angle of fire percentages, instead of trigonometric or corrected angle percentages.
WWII also saw the advent of "hollow charge" or "shaped charge" ammunition, such as the bazooka or panzerfaust rockets. Artillery pieces in the German and American armies had such ammo, normally called HEAT (high explosive anti-tank). HEAT type rounds have a constant penetration value proportional to the size of the warhead, and thus armor penetration doesn't change with range, eliminating complex calculations. However, HEAT does tend to bounce off sloped armor very easily, and has an extremely difficult time against rounded armor. Worse, when fired from a rifled gun (any conventional tank or artillery piece is rifled) the rotation of the round reduces accuracy and increases the chance of a bounce. Modern HEAT rounds often have pop-out fins to stop their rotation and stabilize the flight, and the French have gone so far as to develop a counter-rotating round with excellent performance. The Russians have gone over to smooth bore guns, which eliminates the whole problem from the start. These same smooth-bores can also fire APDS, because the bolt inside the shell case has tiny vanes on it to make sure its flight stays stable and accurate. The Russian 115mm gun performed very well on the T-62 in the 1973 war, and the new 125mm is expected to be even better. The British and Germans are now busily designing smooth-bores for the 1980's.
HESH and HEP ammunition, or "squash head" rounds that depend on special explosion-armor inter- actions to cause damage sometimes without physical penetration are really a variation on the HEAT con- cept. The well-made British and American ammunition of this type is often as good if not better than HEAT, but suffers because it has virtually no anti-personnel ability, while HEAT at least has marginal abilities in this area.
CAVEATS
The ballistics equations and table given here are simple, and do not account for two potentially important factors: trajectories with significant arcs, and specially shaped shells. This is because the K values are an exponential function of the shell's terminal velocity (speed at which it hits, at a given range), and many outside factors can influence this velocity. In fact computing this velocity is probably the single biggest ballistics problem, and one that is never truly solved.
The firing trajectory is relatively minor in practice because only guns with a very low muzzle velocity firing at very long ranges, must use any significant elevation. But if they do the shell will come down at an even steeper angle. Since the K value chart is based on the horizontal component of a shell's speed shells arriving at an angle are cheated of non-ho;izontal components, and actually should be going faster. In practice, this rarely adds more than 5-15% to an already weak-penetrating shell. But for those interested, the K value should be multiplied by the following:
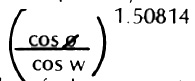
where p = angle of departure (number of degrees the gun is elevated in effect) and w = angle of fall (angle at which the shell is descending, compared to the horizontal).
Unfortunately, you need rather complex equations and tables to compute either angle, found in ballistics books and tables. Therefore, consider yourself lucky you aren't dealing with naval gunnery, where the long ranges involved invariably make these angles a major consideration!
The second problem, shell shape, has a much greater effect, but can be determined if you have any actual penetration data. Basically, a better shaped shell will retain more velocity at a given range, a poorer shaped shell will lose velocity faster than normal, and have less at a given range. This means the K value will change. The trick is determining the degree of change, and applying it at any range.
To work it out, first note the "true" range and penetration result found through your historical re- search. Next, work out the penetration result using the equation and table here. If there is a difference (there usually is, since no shell can be expected to be precisely average), figure out what the K value would be in each case. With the "true" K value, now interpolate to find the "table range" you actually need to get the "true" result. By comparing the "true table range" to the "normal" one you would use you have found the ballistic coefficient of the shell which can then be applied to any range.
If this sounds complicated, you might be comforted to know that this is exactly how one must do it using "real" ballistic equations and tables, and unfortunately there are no short cuts. In addition, this can become even more complex than the foregoing. If we have actual penetration statistics to compare with the results of the formula, then it is possible to determine how much the actual shell departs from the "average" shell used in determining the table of values for K.
To do this, use the actual penetration value at a given range to determine the "actual" K value which would have to be used in the equation to give the correct result. It is then necessary to interpolate where this K value falls on the table for this muzzle velocity. By taking the ratio of the interpolated range corresponding to this actual K value to the actual range, you can determine a range correction factor which can be used for all ranges by taking the actual range and multiplying it by the correction factor before looking up a value for K in the table. Note that a mere ratio of the K values is not useful due to the fact that the fall off in K is not linear with range.
As a matter of general information, the basic armor penetration equation used here is from that used by the U.S. Navy during WWII, which was:
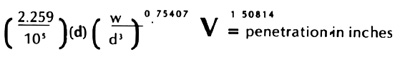
where v = terminal velocity of the shell in feet/second. There are many secondary and minor functions that influence terminal velocity, including air density changes with the barometric pressure, additional modifiers in high angle fire as the shell goes up into thinner air, and a special modification if the firing angle exceeds 10 degrees, since the integral used in computing the ballistic coefficient assumes a flat trajectory, so a correction is needed in the coefficient for higher angle fire [the correction is multiplying the coefficient by 1/(sq. root of sec 0) for those interested]. All these factors are important in naval gunnery, and could be important if determining the penetration ability of howitzers or mortars using high-angle fire.
In the meantime, for those "typical" cases that bedevil the wargamer, the equation and table here provide a fine method for finding "average" performance within a 10% error margin, and when the ballistic coefficient for a specific gun and shell can be found and used, will provide a relatively exact penetration value for almost any range, other than very low-velocity guns shooting a couple thousand yards or more.
ROD BURR COMMENTS
The formula given in Arnold's article is only accurate for face hardened armor. While many, if not most, tanks during World War II had this type of armor, most actual penetration statistics I have seen have been for homogeneous armor. Attempting to force the face hardened formula to fit the data for homogeneous armor can be very frustrating and misleading.
The formula for homogeneous armor, from reference 1, can be given as follows:
Where C is a constant reflecting the quality of the homogeneous armor, T is the thickness of armor penetrated, and the other variables are as given in Arnold's article. This is set up for all English units. An average value for C is 665, according to reference 1, but it is probably best to actually determine the quality of the armor used for specific tests from the experimental data given when comparing the results of the formula with measured data. As an example of this, I used the penetrations listed in the appendix of reference 2, and calculated the value of C for the Pak 38. I then assumed that the same quality of armor had been used for tests of the other weapons listed and found the results verified this.
In order to simplify the calculations, l determined that the conversion factor to express the equation in metric units was to multiply the formula by 3.6994585. This was convenient due to the fact that all units given in the appendix were metric (weight in KG, MV in M/sec, and D in CM). The projectile weight for the Pak 38 was 2.25 KG, the muzzle velocity was 823 m/see, and the diameter was 5 cm. Using the average value of 665 for C, the predicted penetration at 0 m range is 79 mm of armor, compared to a measured value of 99. We can then use this ratio (99/79) as a correction factor for the actual armor used in the test. Using this correction for the 7.5 cm Pak 40, which had a muzzle velocity of 750 m/see, and a weight of 6.8 kg, gives a predicted penetration of 146.7 versus an actual penetration of 149 mm. For the 8.8 cm Pak 43, with a mv of 1000 m/see and a weight of 10.16 kg, the predicted versus actual penetration is 228 mm versus 225 mm. All these results are for 0 m range. At the moment I have no data available that gives the drop off in shell velocity with range, so I have been unable to compare predictions at longer ranges. Given this type of data, I would expect the formula to give results agreeing with the measured ones.
REFERENCES
1. Okun, Nathan, "Armor and Its Application to Warships", 3 parts published in WARSHIP INTERNATIONAL during 1976 (issues unknown). This article provides an excellent description of armor and projectile types, and a comprehensive description (in Part 2) of the various formulas to be used for different types of armor. The article is a general description of armor penetration, and is not restricted to warships in applicability. The calculations done for homogeneous armor are entirely based on material from this article. My thanks to Byron Angel, THE COURIER naval editor, for calling my attention to it.
Von Senger und Etterrlin, F.M., GERMAN TANKS OF WORLD WAR II, Stackpole Books, Harrisburg, PA (1969). This book is an excellent description of the development of German armored vehicles, and provides extensive data on armor thickness, weapon performance, and other information in extensive appendices. The figures used for actual penetrations are from this book.
Diehl, Mark, series of articles in AFV-G2 on armor and armor penetration. Volume 3, no. 8 & 9 had "behind the Armor vs. Shot Confrontation" which described some of the basic factors determining the effectiveness of armor and armor peircing rounds. Following this was a series of articles on actual penetrations for several German weapons (Vol. 3, No. 12 - 88mm, Vol. 4 no. 2 - 75mm, Vol. 4, no. 4 - 37mm & 50mm, and vol. 4, no. 7 - 128 mm). Each of these articles covers all the German weapons of the given caliber, and lists the types of ammunition, with statistics, available for each weapon.
Letter to Editor Rebuttal (Vol. II No. 3)
Back to Table of Contents -- Courier Vol. 2 #1
To Courier List of Issues
To MagWeb Master Magazine List
© Copyright 1980 by The Courier Publishing Company.
This article appears in MagWeb (Magazine Web) on the Internet World Wide Web.
Other military history articles and gaming articles are available at http://www.magweb.com