Radars work, of course, by putting out a pulse of radio frequency energy and collecting the reflected return from a target. While the concept is simple, the details of implementing a modern radar system are more involved. If you have read anything about radar systems, you have probably come across terms such as PRF (pulse repetition frequency), pulse Doppler, MTI (moving target indication), and track-whilescan. If you are into somewhat more esoteric literature, you may have seen terms such as range and velocity ambiguities, pulse compression techniques, synthetic apertures, and digital signal processing. The lexicon of the radar community can be somwhat intimidating, but the underlying concepts are not too difficult. This article is directed at the Air Superiority gamer who wants to get a better understanding of simple radar deign principles, and a realistic set of radar rules for his game. Simple, basic laws of physics are at the heart of all the complexity of the radar world. Energy is generated by the radar transmitter and is radiated into space by an antenna. The antenna acts as an energy concentrator, focusing it into a narrower beam than would be possible without it. As this energy flies through the air ahead of the aircraft, it spreads out. The rule is that the energy per unit area in the beam falls off like one over the square of the distance travelled. This "inverse square law" should be familiar to those who have had a basic physics course which mentions gravity. When the spreading beam strikes the target, a portion is reflected. The amount of energy reflected depends on the amount in the beam and the effective size of the target. This effective size is known as the target's "radar cross-section". Real radar cross-sections are complex beasts which are very sensitive to the orientation of the target and the frequency of the radar pulse, but typical values are about I square meter for an ordinary fighter, 5 square meters for a large fighterbomber, and as much as 100 square meters for an intercontinental bomber, such as the B-52. Stealth aircraft have been modified to reduce their cross-sections to values of 0.05 square meters or less. Once the energy is reflected from the target, it must fly back to the receiver. As is does so, it spreads out again, following the same inverse square law as the transmitted pulse. The combination of the two trips results in an overall "one over distance to the fourth" law for radar effective ranges. Upon returning to the transmitter, the antenna comes into play again, this time as an energy concentrator and collector. Usually the same antenna is used for both receiving and transmitting, so you can see that it is extremely important to have an optimal antenna design. A lot of books have been written on antenna design and the requirement to pack the best possible antenna into the nose of an aircraft places severe constraints on the radar designer. This is one of the sources of the significant differences in radar performance observed in modern aircraft. It's not an easy job. Once the energy has entered to the receiver, it must be detected. The powerful electronics generate noise in the receiver which can mimic real signals. If the receiver is made too sensitive, there will be many "false alarms". If it is made too insensitive, it will miss genuine targets. Once again, the radar system designer is forced to compromise. The choices made can spell the difference between an accurate, effective radar, and a piece of junk. Without knowing the details of the transmitter power, antenna gain, and receiver signal-to-noise ratio, we cannot make predictions of the effective range of a radar. These details can often be found in publications like Jane's or Aviation Week and Space Technology if you're willing to do a little digging. What we can do without that information, however, is make a table of ranges for various probabilities of detection, given a reasonable guess of some realistic minimum detection range. 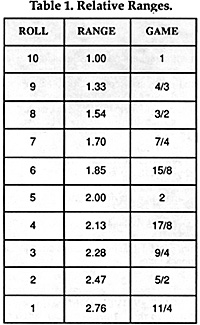Table 1 shows a list of effective range multipliers relative to "auto" detection range. The RANGE column shows the effective range, relative to the minimum, for the various die rolls (1 to 10) needed for a detection. The GAME column contained rounded, approximate values more suited for game play in Air Superiority. Standard Air Superiority radar rules give a base 100% probability of detection at a range, in hexes, equal to the search strength of the radar being used. The radar table then imposes a -1 penalty for every multiple of that base range. As you can see from the table, the actual probability of detection falls off much faster: down to 50% at twice the minimum range. At three times the minimum, the true probability of detection is down to about 1.5% (for purists in the crowd, all this assumes a 95% probability of detection at the "autodetect" range). To use Table I in a game, you need only multiply all the numbers in the GAME column by the search strength of the radar. As an example, an aircraft with a search strength of 40 would need a 10 to detect targets out to 40 hexes, a 9 to detect targets from 41 to 53 hexes, an 8 for targets between 54 and 60 hexes distant, and so on. The maximum detection range would be 110 hexes and beyond this range, the radar would be ineffective. It is certainly possible to rewrite the radar range chart using this system, but I'll leave that to the dedicated reader. As you can see, this greatly reduces the useful ranges for radars and gives a significant advantage to aircraft with more powerful radar systems, as is actually the case. What about the other pulse parameters we talked about? A detailed discussion would take us too far afield, but at least one point should be made. A radar's maximum range is often limited, not by its power or antenna, but by the separation in time between pulses, the so-called "pulse repetition interval" or PRI. Numerically, the PRI is one over the PRF, a value which can often be found in Jane's. (A radar with a 20 KHz PRF would have 50 ps PRI). The reason this value limits the range is that the radar cannot distinguish between pulses that return before or after the next outgoing pulse. The target could be close, returning a pulse immediately, or it could be farther away, returning a pulse at the PRI plus some amount. The speed of light is the governing factor here. Rule of thumb: the maximum unambiguous range for a radar in nautical miles is equal to one twelfth of its PRI in microseconds. In the example above, the radar would have a maximum unambiguous range of about 4 nautical miles. It would seem that the answer to the problem would be to space the pulses further apart, but that leads to other difficulties when vying to track targets (where frequent updates of position and velocity are needed). There are advanced techqniues for getting around this limitation that involve changing the frequency or shape of successive pulses so the radar can determine which pulse a given return came from, but each such fix introduces other problems. If you'd like to know more, get a copy of Radar Principles for the Non-Specialist by J. C. Toomay. It's a very readable work and will give you a much better understanding of modern radar techniques. Back to Table of Contents -- Air Power # 11 Back to Air Power List of Issues Back to MagWeb Magazine List © Copyright 1990 by J.D. Webster This article appears in MagWeb.com (Magazine Web) on the Internet World Wide Web. Other articles from military history and related magazines are available at http://www.magweb.com